Question

如图所示，在POQ区域内分布有磁感应强度为B=0.5T的匀强磁场，磁场方向垂直纸面向里，一束带负电的粒子流沿纸面垂直于磁场边界OQ方向从A点射入磁场，已知 OA=L=0.4m，∠POQ=θ=45°，粒子质量为m=8.0×10^-6kg，电荷量q=2.0×10^-2C，要使粒子不从OP边射出，求粒子流进入磁场时的最大速度？不计粒子的重力．

Answer 1

分析：粒子仅在洛伦兹力作用下做匀速圆周运动，由左手定则可得粒子将向右发生弯曲，当粒子恰好在磁场上边界与OP相切时粒子的速度最大，由几何关系确定已知长度与轨道半径的关系，从而根据半径公式，可求出粒子的最大速度．

解答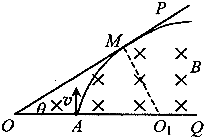：解：粒子进入匀强磁场后做匀速圆周运动，并向右弯曲，当圆轨道与OP边相切时，射入磁场的粒子速度最大，
设圆轨道圆心为0₁，切点为M，半径为r，粒子最大速度为v_m，如图所示，
由洛伦兹力提供向心力：qvB=

m v 2 m

r

则r=

mvm

qB

…①
由几何关系得：

r

L+r

=sinθ…②
整理得：r=(

2

+1)L…③
vm=

( 2 +1)qBL

m

…④
代入数据解得：vm=1.2×103m/s…⑤
答：粒子流进入磁场时的最大速度vm=1.2×103m/s

点评：根据粒子在洛伦兹力作用下做匀速圆周运动，依据几何特性作图是解题的关键之处．是典型的数理结合的题型．