题目内容
13.“探月热”方兴未艾,我国研制的月球卫星“嫦娥二号”已发射升空,已知月球质量为M,半径为R.引力常量为G,以下说法正确的是( )| A. | 在月球上以初速度v0竖直上抛一个物体,物体上升的最大高度为$\frac{2{R}^{2}{v}_{0}^{2}}{GM}$ | |
| B. | 在月球上以初速度v0竖直上抛一个物体,物体落回到抛出点所用时间为$\frac{2{R}^{2}{v}_{0}}{GM}$ | |
| C. | 在月球上发射一颗绕它沿圆形轨道运行的卫星的最大运行速度为$\sqrt{\frac{R}{GM}}$ | |
| D. | 在月球上发射一颗绕它沿圆形轨道运行的卫星的最大周期为2π$\sqrt{\frac{R}{GM}}$ |
分析 忽略月球自转的影响,根据万有引力等于重力列出等式求出月球表面的重力加速度.
根据竖直上抛的运动规律求解.
研究卫星绕月球做圆周运动,根据万有引力提供向心力,列出等式求解.
解答 解:A、已知月球质量为M,半径为R.引力常量为G,忽略月球自转的影响,根据万有引力等于重力列出等式:
$\frac{GMm}{{R}^{2}}$=mg
g=$\frac{GM}{{R}^{2}}$
在月球上以初速度v0竖直上抛一个物体,物体上升的最大高度为:h=$\frac{{v}_{0}^{2}}{2g}$=$\frac{{R}^{2}{v}_{0}^{2}}{2GM}$.故A错误.
B、在月球上以初速度%竖直上抛一个物体,物体落回到抛出点所用时间为:t=$\frac{{2v}_{0}}{g}$=$\frac{{2R}^{2}{v}_{0}}{GM}$,故B正确.
C、研究卫星绕月球做圆周运动,根据万有引力提供向心力,列出等式
$\frac{GMm}{{r}^{2}}$=$\frac{m{•4π}^{2}r}{{T}^{2}}$=$\frac{{mv}^{2}}{r}$
T=2πr$\sqrt{\frac{r}{GM}}$
v=$\sqrt{\frac{GM}{r}}$
当轨道半径r取月球半径R时,
卫星的最小周期为2πR$\sqrt{\frac{R}{GM}}$,卫星的最大运行速度为$\sqrt{\frac{GM}{R}}$,故C错误,D错误.
故选:B.
点评 把星球表面的物体运动和天体运动结合起来是考试中常见的问题.向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

练习册系列答案
相关题目
18.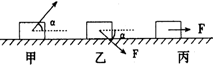 如图所示,甲、乙、丙三个物体质量相同,与地面的动摩擦因数相同,受到三个大小相同的作用力F而运动,则它们受到摩擦力大小关系是( )
如图所示,甲、乙、丙三个物体质量相同,与地面的动摩擦因数相同,受到三个大小相同的作用力F而运动,则它们受到摩擦力大小关系是( )
 如图所示,甲、乙、丙三个物体质量相同,与地面的动摩擦因数相同,受到三个大小相同的作用力F而运动,则它们受到摩擦力大小关系是( )
如图所示,甲、乙、丙三个物体质量相同,与地面的动摩擦因数相同,受到三个大小相同的作用力F而运动,则它们受到摩擦力大小关系是( )| A. | 三者相同 | B. | 乙最大 | ||
| C. | 丙最大 | D. | 条件不足无法确定 |
5.关于物体运动状态的改变,下列说法中正确的是( )
| A. | 运动物体的加速度不变,则其运动状态一定不变 | |
| B. | 物体的位置在不断变化,则其运动状态一定在不断变化 | |
| C. | 做直线运动的物体,其运动状态一定不变 | |
| D. | 运动物体的速度不变,其运动状态一定不变 |
3.一个人的质量为50kg,站在电梯中,当电梯从静止开始以 2m/s2的加速度匀加速上升了10m时,取g=10m/s2,则此过程( )
| A. | 人的动能增加了1000J | B. | 人的动能增加了5000 J | ||
| C. | 人的机械能增加了5000 J | D. | 电梯对人做功6000 J |
 一个滑块质量2kg,在光滑斜面上由A滑到B,如图所示.已知AB=40cm,斜面对物体支持力是17N,求:在A到B的过程中,重力和支持力各做功多少?
一个滑块质量2kg,在光滑斜面上由A滑到B,如图所示.已知AB=40cm,斜面对物体支持力是17N,求:在A到B的过程中,重力和支持力各做功多少?