题目内容
1. 如图所示,水平光滑细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为mA和mB,由于B球受到水平风力作用,环A与B球一起向右匀加速运动,已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )
如图所示,水平光滑细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为mA和mB,由于B球受到水平风力作用,环A与B球一起向右匀加速运动,已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )| A. | 轻质绳对B球的拉力为$\frac{{m}_{A}g}{cosθ}$ | |
| B. | 匀加速的加速度大小为$\frac{{m}_{B}tanθ}{{m}_{A}}$ | |
| C. | 杆对A球的支持力随着风力的增加而减小 | |
| D. | 若风力增大时,轻质绳与竖直方向的夹角θ一定增加 |
分析 分别对AB两球及整体进行分析,利用正交分解法可明确水平和竖直两个方向上的受力情况,再对水平方向由牛顿第二定律进行分析求解.
解答 解:对球B受力分析,受重力、拉力和水平风力,如图
对小球B分析可知,B球竖直方向受力平衡;
则有:Tcosθ=mBg;
T=$\frac{{m}_{B}g}{cosθ}$,故A错误;
B、对A受力分析可知,A在水平方向受到的拉力为:Tsinθ,由牛顿第二定律可知:
Tsinθ=mAa
解得:a=$\frac{{m}_{B}gtanθ}{{m}_{A}}$,故B正确;
C、对整体分析可知,在竖直方向整体受力平衡,故水平风力增大时不会改变杆对A球的作用力,故C错误;
D、风力增大时,整体的加速度增大,故拉力在水平方向上的分力增大,而竖直方向分力不变;故夹角增大,故D正确;
故选:BD
点评 本题考查牛顿第二定律的应用,要注意选择研究对象,用好正交分解法进行分析.

练习册系列答案
相关题目
10.关于初速度等于零的匀加速直线运动,下列说法中正确的是( )
| A. | 速度与运动时间成正比 | |
| B. | 速度的增量与运动时间的平方成正比 | |
| C. | 位移与运动时间的平方成正比 | |
| D. | 在连续相同时间内的位移之差都相同 |
12. 一条直导线平行于通电螺线管的轴线放在螺线管的正上方,如图所示,导线ab通以由b向a的电流,则导线ab的可能运动是( )
一条直导线平行于通电螺线管的轴线放在螺线管的正上方,如图所示,导线ab通以由b向a的电流,则导线ab的可能运动是( )
 一条直导线平行于通电螺线管的轴线放在螺线管的正上方,如图所示,导线ab通以由b向a的电流,则导线ab的可能运动是( )
一条直导线平行于通电螺线管的轴线放在螺线管的正上方,如图所示,导线ab通以由b向a的电流,则导线ab的可能运动是( )| A. | 导线ab不做任何运动 | |
| B. | 导线ab向纸面内平移 | |
| C. | 导线a端向纸外,b端向纸内转动,同时向下移动 | |
| D. | 导线a端向纸内,b端向纸外转动,同时向上移动 |
9.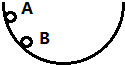 如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )
如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )
 如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )
如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )| A. | vA<vB | B. | FA<FB | C. | aA<aB | D. | ωB<ωA |
6.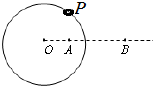 如图,一个由绝缘材料做成的圆环水平放置,O为圆心,一带电小珠 P穿在圆环上,可沿圆环无摩擦的滑动.在圆环所在的水平面内有两个点电荷 Q1、Q2分别位于A、B两点,A点位于圆环内.B点位于圆环外,O、A、B三点位于同一直线上.现给小珠P一初速度,P沿圆环做匀速圆周运动.则以下判断正确的是( )
如图,一个由绝缘材料做成的圆环水平放置,O为圆心,一带电小珠 P穿在圆环上,可沿圆环无摩擦的滑动.在圆环所在的水平面内有两个点电荷 Q1、Q2分别位于A、B两点,A点位于圆环内.B点位于圆环外,O、A、B三点位于同一直线上.现给小珠P一初速度,P沿圆环做匀速圆周运动.则以下判断正确的是( )
 如图,一个由绝缘材料做成的圆环水平放置,O为圆心,一带电小珠 P穿在圆环上,可沿圆环无摩擦的滑动.在圆环所在的水平面内有两个点电荷 Q1、Q2分别位于A、B两点,A点位于圆环内.B点位于圆环外,O、A、B三点位于同一直线上.现给小珠P一初速度,P沿圆环做匀速圆周运动.则以下判断正确的是( )
如图,一个由绝缘材料做成的圆环水平放置,O为圆心,一带电小珠 P穿在圆环上,可沿圆环无摩擦的滑动.在圆环所在的水平面内有两个点电荷 Q1、Q2分别位于A、B两点,A点位于圆环内.B点位于圆环外,O、A、B三点位于同一直线上.现给小珠P一初速度,P沿圆环做匀速圆周运动.则以下判断正确的是( )| A. | Q1与Q2为同种电荷 | |
| B. | 对于由Q1、Q2产生的电场,在圆环上电势处处相等 | |
| C. | 对于由Q1、Q2产生的电场,在圆环上电场强度处处相等 | |
| D. | 小珠P运动过程中对圆环的弹力大小处处相等 |
13.一物体从静止出发,沿一条直线运动的v-t图象如图所示,下列说法中正确的是( )


| A. | 物体一直沿一个方向运动 | |
| B. | 物体的加速度的大小总是变化的 | |
| C. | 物体做往返的运动,永远不会停下来 | |
| D. | 物体每次返回的路程都减少一点,所以最终会停下来 |
10.两个分别带有电荷量-2Q和+3Q的相同金属小球(均可视为点电荷),固定在相距为r的两处,它们间库仑力的大小为F.两小球相互接触后将其固定距离变为$\frac{r}{2}$,则两球间库仑力的大小为( )
| A. | $\frac{1}{6}$F | B. | $\frac{1}{12}$F | C. | 6F | D. | 12F |
11.关于波的图象,下列说法中正确的是( )
| A. | 横坐标轴x表示波的传播方向上各质点的平衡位置 | |
| B. | 横坐标轴x表示质点距波源的距离 | |
| C. | 纵坐标轴y表示某一时刻各个质点偏离平衡位置的位移 | |
| D. | 坐标原点一定是波源的位置 |
 粗糙的地面上放着一个质量M=1.5kg的斜面,斜边部分光滑,底面与地面的动摩擦因数μ=0.2,倾角θ=37°,在固定在斜面的挡板上用轻质弹簧连接一质量m=0.5kg 的小球,弹簧劲度系数k=200N/m,现给斜面施加一水平向右为F的恒力作用,使整体向右以a=1m/s2匀加速运动.
粗糙的地面上放着一个质量M=1.5kg的斜面,斜边部分光滑,底面与地面的动摩擦因数μ=0.2,倾角θ=37°,在固定在斜面的挡板上用轻质弹簧连接一质量m=0.5kg 的小球,弹簧劲度系数k=200N/m,现给斜面施加一水平向右为F的恒力作用,使整体向右以a=1m/s2匀加速运动.