题目内容
 两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h.物块从静止滑下,然后又滑上劈B.
两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h.物块从静止滑下,然后又滑上劈B.求:
(1)物体滑离A后A的速度大小.
(2)物块在B上能够达到的最大高度.
分析:(1)物块从A上下滑过程中,物块与A组成的系统机械能守恒,水平方向动量守恒,根据两大守恒定律求解物体滑离A后A的速度大小.
(2)物块滑上B的过程中,当两个物体的速度相同时,B上升到最大高度,由物块和B组成的系统机械能守恒,水平方向动量也守恒,即可求得物块在B上能够达到的最大高度..
(2)物块滑上B的过程中,当两个物体的速度相同时,B上升到最大高度,由物块和B组成的系统机械能守恒,水平方向动量也守恒,即可求得物块在B上能够达到的最大高度..
解答:解:设物块到达劈A的底端时,物块和A的速度大小分别为v和V,由机械能守恒和动量守恒得
mgh=
mv2+
M1V2 ①
M1V-mv=0 ②
解得,v=
,V=
(2)设物块在劈B上达到的最大高度为H,此时物块和B的共同速度大小为V',由机械能守恒和动量守恒得
mgH+
(M2+m)V′2=
mv2 ③
mv=(M2+m)V'④
联立得 H=
h
答:(1)物体滑离A后A的速度大小是
.
(2)物块在B上能够达到的最大高度
h.
mgh=
| 1 |
| 2 |
| 1 |
| 2 |
M1V-mv=0 ②
解得,v=
|
| m |
| M1 |
|
(2)设物块在劈B上达到的最大高度为H,此时物块和B的共同速度大小为V',由机械能守恒和动量守恒得
mgH+
| 1 |
| 2 |
| 1 |
| 2 |
mv=(M2+m)V'④
联立得 H=
| M1M2 |
| (M1+m)(M2+m) |
答:(1)物体滑离A后A的速度大小是
| m |
| M1 |
|
(2)物块在B上能够达到的最大高度
| M1M2 |
| (M1+m)(M2+m) |
点评:本题首先要分析物体的运动过程,确定研究对象,第一个过程以物块与A为研究对象,第二过程以物块与A为研究对象;其次根据系统的机械能守恒和水平方向动量守恒,就很容易解答.

练习册系列答案
相关题目
 两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h。物块从静止滑下,然后又滑上劈B。求物块在B上能够达到的最大高度?
两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h。物块从静止滑下,然后又滑上劈B。求物块在B上能够达到的最大高度? 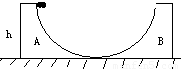
 两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h。物块从静止滑下,然后又滑上劈B。求物块在B上能够达到的最大高度?
两质量分别为M1和M2的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h。物块从静止滑下,然后又滑上劈B。求物块在B上能够达到的最大高度?