题目内容
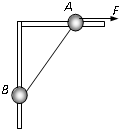 (2004?南通三模)如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.20,杆的竖直部分光滑,两部分各套有质量分别为2.0kg和1.0kg的小球A和B,A、B间用细绳相连,初始位置OA=1.5m,OB=2.0m,g取10m/s2,则
(2004?南通三模)如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.20,杆的竖直部分光滑,两部分各套有质量分别为2.0kg和1.0kg的小球A和B,A、B间用细绳相连,初始位置OA=1.5m,OB=2.0m,g取10m/s2,则(1)若用水平拉力F1沿杆向右缓慢拉A,使之移动0.5m,该过程中A受到的摩擦力多大?拉力F1做功多少?
(2)若小球A、B都有一定的初速度,A在水平拉力F2的作用下,使B由初始位置以1.0m/s的速度匀速上升0.5m,此过程中拉力F2做功多少?
分析:(1)先对AB整体受力分析,受拉力F、总重力G、支持力N、向左的摩擦力f和向右的弹力N1,根据共点力平衡条件列式,求出支持力N,从而得到滑动摩擦力为恒力;最后对整体运用能量关系列式,得到拉力做的功.
(2)设细绳与竖直杆的夹角为θ,由于绳子不可伸长,运用速度的分解,有vBcosθ=vAsinθ,可求出B匀速上升0.5m过程A的初速度和末速度,再由能量关系求解拉力F2做功.
(2)设细绳与竖直杆的夹角为θ,由于绳子不可伸长,运用速度的分解,有vBcosθ=vAsinθ,可求出B匀速上升0.5m过程A的初速度和末速度,再由能量关系求解拉力F2做功.
解答:解:(1)先对AB整体受力分析,如图所示.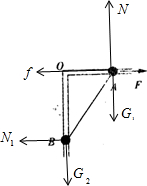
A、B小球和细绳整体竖直方向处于平衡,A受到的弹力为:
N=(mA+mB)g
则A受到的摩擦力为Ff=μ(mA+mB)g
代入数字得:Ff=6N
由几何关系,sB=0.5m
由能量关系,拉力F1做功为:W1=Ffs+mBgsB;
代入数字得:W1=20 J
(2)设细绳与竖直方向的夹角为θ,因细绳不可伸长,两物体沿绳子方向的分速度大小相等,所以有
vBcosθ=vAsinθ
则:A的初速度vA1=vBcotθ1=
m/s
末速度 vA2=vBcotθ2=
m/s
设拉力F2做功为W2,对系统,由能量关系得:W2-FfsB-mBgsB=
mA
-
mA
代入数据得W2=6.8 J
答:
(1)A受到的摩擦力为6N,力F1作功为20J.
(2)力F2作功为6.8J.

A、B小球和细绳整体竖直方向处于平衡,A受到的弹力为:
N=(mA+mB)g
则A受到的摩擦力为Ff=μ(mA+mB)g
代入数字得:Ff=6N
由几何关系,sB=0.5m
由能量关系,拉力F1做功为:W1=Ffs+mBgsB;
代入数字得:W1=20 J
(2)设细绳与竖直方向的夹角为θ,因细绳不可伸长,两物体沿绳子方向的分速度大小相等,所以有
vBcosθ=vAsinθ
则:A的初速度vA1=vBcotθ1=
| 4 |
| 3 |
末速度 vA2=vBcotθ2=
| 3 |
| 4 |
设拉力F2做功为W2,对系统,由能量关系得:W2-FfsB-mBgsB=
| 1 |
| 2 |
| v | 2 A2 |
| 1 |
| 2 |
| v | 2 A1 |
代入数据得W2=6.8 J
答:
(1)A受到的摩擦力为6N,力F1作功为20J.
(2)力F2作功为6.8J.
点评:本题中拉力为变力,先对整体受力分析后根据共点力平衡条件得出摩擦力为恒力,然后根据功能关系或动能定理求变力做功.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2004?南通三模)如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°,已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )
(2004?南通三模)如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°,已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( ) (2004?南通三模)在收音机电路中,经天线接收下来的电信号既有高频成分又有低频成分,经放大后,需要把高频成分和低频成分分开,只让低频成分输入下一级,如果采用如图所示的电路,图中虚线框a和b内只用一个电容器或电感器,那么( )
(2004?南通三模)在收音机电路中,经天线接收下来的电信号既有高频成分又有低频成分,经放大后,需要把高频成分和低频成分分开,只让低频成分输入下一级,如果采用如图所示的电路,图中虚线框a和b内只用一个电容器或电感器,那么( )