题目内容
13.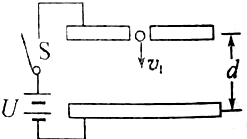 如图所示为密立根油滴实验示意图.在电介质为空气的电容器中,观测以某一速度滴入的油滴.当开关S断开时,从上板小孔飘入的带电油滴能以稳定的速率v1下降.合上S,过一会儿油滴由下降转为上升,稳定时速率为v2.设油滴的质量为m,电源电压为U,板间距离为d,油滴受到空气的黏滞阻力的大小与速度成正比.即Ff=kv(式中k为未知量).
如图所示为密立根油滴实验示意图.在电介质为空气的电容器中,观测以某一速度滴入的油滴.当开关S断开时,从上板小孔飘入的带电油滴能以稳定的速率v1下降.合上S,过一会儿油滴由下降转为上升,稳定时速率为v2.设油滴的质量为m,电源电压为U,板间距离为d,油滴受到空气的黏滞阻力的大小与速度成正比.即Ff=kv(式中k为未知量).(1)求油滴所带的电荷量q.
(2)设两板间距d=0.5cm,板间电压U=150V,测得油滴的直径D=1.10×10-6m,油滴的密度ρ=1.05×103kg/m3,若实验中观察到油滴向下和向上匀速运动的速率相等,试由此计算油滴的电荷量并说明电性.
分析 (1)当平行金属板间不加电压时,油滴最终以速度v1竖直向下匀速运动时,所受的重力与阻力平衡,大小相等,可列出方程,再根据密度公式求出球的质量,联立求出k.当上板带正电,下板带负电,两板间的电压为U时,带电油滴恰好能以速度v2竖直向上匀速运动时,电场力与重力、阻力相平衡,列式可求解.
(2)观察到油滴向下和向上匀速运动的速率相等,由此得出电场力与重力的关系,然后代入(1)的公式,即可解答.
解答 解:(1)由题意得,由于空气阻力大小与速度大小成正比,匀速下降上重力与阻力相等,即:mg=kv1 ①
油滴在电场中缓慢上升时:qE=mg+kv2
联立得:$q=\frac{dk({v}_{1}+{v}_{2})}{U}$=$\frac{dmg({v}_{1}+{v}_{2})}{{v}_{1}U}$ ②
(2)由题意知:闭合开关后粒子受到的电场力大小向上,指向正极板,所以粒子一定是带负电.
测得油滴的直径D=1.10×10-6m,油滴的密度ρ=1.05×103kg/m3,质量:
m=ρV=$ρ•\frac{4}{3}π(\frac{D}{2})^{3}$ ③
实验中观察到油滴向下和向上匀速运动的速率相等,联立①②③将各数据代入公式得带电量:q=4.8×10-19C.
答:(1)油滴所带电量是 $\frac{dmg({v}_{1}+{v}_{2})}{{v}_{1}U}$;(2)油滴的电荷量是4.8×10-19C,带负电.
点评 本题是密立根测量油滴电荷量的实验,实质是平衡问题,根据平衡条件即可求解.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
3.打桩机重锤从距地面5m高处落下,被与地面相平的桩弹回后升到距地面1m高处,若取此处为坐标原点,向上为正方向.则重锤在此过程中通过的路程和发生的位移分别是( )
| A. | 6m-4m | B. | 4m lm | C. | 5m 0 | D. | 6m 4m |
18.关于匀速直线运动.以下说法正确的是( )
| A. | 物体做匀速直线运动时在两段相等时间里通过的位移一定相等 | |
| B. | 物体若在两段相等时间里通过的位移相等.则物体一定做匀速直线运动 | |
| C. | 路程和位移大小始终相等的运动,一定是匀速直线运动 | |
| D. | 速率不变的运动,一定是匀速直线运动 |
7. 如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.下列说法正确的是( )
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.下列说法正确的是( )
 如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.下列说法正确的是( )
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.下列说法正确的是( )| A. | 斜面倾角α=30° | |
| B. | A获得最大速度为$2g\sqrt{\frac{m}{5k}}$ | |
| C. | C刚离开地面时,B的加速度最大 | |
| D. | 从释放A到C刚离开地面的过程中,A、B两小球组成的系统机械能守恒 |
5.关于加速度与速度的关系,正确的说法是( )
| A. | 加速度为零的物体,其速度一定为零 | |
| B. | 加速度减小时,速度一定减小 | |
| C. | 2 m/s2的加速度比-4m/s2的加速度小 | |
| D. | 速度为零,加速度为零 |
 如图所示电路,R1=1Ω,R2=2Ω,R3=3Ω,a、b间电压为5V.当S断开时,c、d间电压为2V,当S闭合时,c、d间电压为0V.
如图所示电路,R1=1Ω,R2=2Ω,R3=3Ω,a、b间电压为5V.当S断开时,c、d间电压为2V,当S闭合时,c、d间电压为0V. 如图所示,A,B两物体叠放在一起,由静止释放后沿光滑斜面下滑,且始终保持相对静止,B上表面水平,则物体B的受力示意图是( )
如图所示,A,B两物体叠放在一起,由静止释放后沿光滑斜面下滑,且始终保持相对静止,B上表面水平,则物体B的受力示意图是( )