题目内容
14.如图所示,两平行金属板水平放置,板间存在着如图所示的交变电场,极板长为L,板间距离为d,取竖直向上的方向为电场强度的正方向.一带电量为q的正电荷从两板正中间的位置由左侧射入板间.初速度为v0,己知电荷所受电场力大小是其重力的2倍.重力加速度为g,且0时刻射入的粒子正好可从板间射出.求: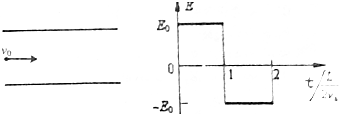
(1)两板间距d应满足的条件;
(2)0时刻射入的粒子射出板间时的动能.
分析 (1)将电荷的运动分解为水平方向和竖直方向,在水平方向上做匀速直线运动,在竖直方向上,结合受力,根据牛顿第二定律和运动学公式求出最大位移的大小,从而得出d满足的条件.
(2)根据竖直方向上的运动规律,结合运动学公式求出末时刻竖直方向的分速度,结合平行四边形定则求出射出时的动能.
解答 解:(1)0-$\frac{L}{2{v}_{0}}$内,电荷所受的电场力方向竖直向上,根据牛顿第二定律得,${a}_{1}=\frac{q{E}_{0}-mg}{m}=g$,
则粒子向上运动的位移${y}_{1}=\frac{1}{2}{a}_{1}{t}^{2}=\frac{1}{2}g×\frac{{L}^{2}}{4{{v}_{0}}^{2}}=\frac{g{L}^{2}}{8{{v}_{0}}^{2}}$,
粒子的速度${v}_{y}={a}_{1}t=\frac{gL}{2{v}_{0}}$,
$\frac{L}{2{v}_{0}}-\frac{L}{{v}_{0}}$内,电荷所受的电场力方向竖直向下,根据牛顿第二定律得,${a}_{2}=\frac{q{E}_{0}+mg}{m}=3g$,
向上速度减为零的时间$t′=\frac{{v}_{y}}{{a}_{2}}=\frac{L}{6{v}_{0}}$$<\frac{L}{2{v}_{0}}$,知在竖直方向上粒子向上做匀减速运动到零后再向下做匀加速运动,
向上匀减速运动的位移${y}_{2}=\frac{{{v}_{y}}^{2}}{2{a}_{2}}=\frac{\frac{{g}^{2}{L}^{2}}{4{{v}_{0}}^{2}}}{6g}$=$\frac{g{L}^{2}}{24{{v}_{0}}^{2}}$,
可知$\frac{d}{2}$$≥{y}_{1}+{y}_{2}=\frac{g{L}^{2}}{6{{v}_{0}}^{2}}$.
则$d≥\frac{g{L}^{2}}{3{{v}_{0}}^{2}}$.
(2)粒子射出复合场时,竖直方向的分速度${v}_{y}′={v}_{y}-{a}_{2}\frac{L}{2{v}_{0}}=-\frac{gL}{{v}_{0}}$,负号表示方向.
则射出时的动能${E}_{k}=\frac{1}{2}m({{v}_{0}}^{2}+{v}_{y}{′}^{2})$=$\frac{1}{2}m({{v}_{0}}^{2}+\frac{{g}^{2}{L}^{2}}{{{v}_{0}}^{2}})$.
答:(1)两板间距d应满足的条件为$d≥\frac{g{L}^{2}}{3{{v}_{0}}^{2}}$.
(2)0时刻射入的粒子射出板间时的动能为$\frac{1}{2}m({{v}_{0}}^{2}+\frac{{g}^{2}{L}^{2}}{{{v}_{0}}^{2}})$.
点评 本题考查电荷在复合场中的运动,知道前一段时间和后一段时间内竖直方向的加速度不同,结合牛顿第二定律和运动学公式综合求解.

 甲、乙、丙三个物体同时同地出发做直线运动,它们的位移-时间图象如图所示,在20s内它们的平均速度和平均速率的大小关系是( )
甲、乙、丙三个物体同时同地出发做直线运动,它们的位移-时间图象如图所示,在20s内它们的平均速度和平均速率的大小关系是( )| A. | 平均速度大小相等 | B. | 平均速率$\overline{v}$甲>$\overline{v}$乙=$\overline{v}$丙 | ||
| C. | 平均速率$\overline{v}$甲>$\overline{v}$丙>$\overline{v}$乙 | D. | 平均速度和平均速率大小均相等 |
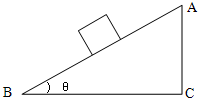
| A. | 箱子可能匀速下滑 | B. | 箱子仍将加速下滑,加速度减小 | ||
| C. | 箱子仍将加速下滑,加速度不变 | D. | 箱子仍将加速下滑,加速度增加 |
| A. | -5m/s | B. | 0 | C. | 5m/s | D. | -10m/s |
 一个重力不计的带电粒子射人电场线分布如图所示的电场中,先后经过M、N两点,运动轨迹用虚线表示.下列说法中正确的是( )
一个重力不计的带电粒子射人电场线分布如图所示的电场中,先后经过M、N两点,运动轨迹用虚线表示.下列说法中正确的是( )| A. | 带电粒子带正电 | |
| B. | 带电粒子在M点的动能比在N点的大 | |
| C. | 带电粒子在M点的加速度比在N点的大 | |
| D. | 带电粒子在M点的电势能比在N点的大 |
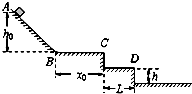 如图,一小滑块从光滑斜面上高h0=0.8m的A点由静止滑下.斜面AB与水平面BC在B处通过一小圆弧光滑连接.长x0=1.2m的水平面BC与滑块之间的动摩擦因数μ=0.5,C点右侧还有一级台阶,D点右侧是较长的水平地面.台阶的高度均为h=0.2m,宽为L=0.35m.求:
如图,一小滑块从光滑斜面上高h0=0.8m的A点由静止滑下.斜面AB与水平面BC在B处通过一小圆弧光滑连接.长x0=1.2m的水平面BC与滑块之间的动摩擦因数μ=0.5,C点右侧还有一级台阶,D点右侧是较长的水平地面.台阶的高度均为h=0.2m,宽为L=0.35m.求:
 像打点计时器一样,光电计时器也是一种研究物体运动情况的常用计时仪器,其结构如图所示.a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.现有一放在气垫导轨上的滑块通过光电门,滑块上装了一个宽度为d=3.0cm的遮光片,滑块在牵引力作用下先后通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为△t1=0.29s,通过第二个光电门的时间为△t2=0.11s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t=3.57s,则滑 块经过第一个光电门时的速度v1=0.10m/s经第二个光电门的速度v2=0.27m/s滑块的平均加速度约为:0.045m/s2(结果保留两位有效数字)
像打点计时器一样,光电计时器也是一种研究物体运动情况的常用计时仪器,其结构如图所示.a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.现有一放在气垫导轨上的滑块通过光电门,滑块上装了一个宽度为d=3.0cm的遮光片,滑块在牵引力作用下先后通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为△t1=0.29s,通过第二个光电门的时间为△t2=0.11s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t=3.57s,则滑 块经过第一个光电门时的速度v1=0.10m/s经第二个光电门的速度v2=0.27m/s滑块的平均加速度约为:0.045m/s2(结果保留两位有效数字)