题目内容
已知地球半径为R,地球表面重力加速度为g,万有引力常量为G,不考虑地球自转的影响.
(1)求卫星环绕地球运行的第一宇宙速度v1;
(2)若卫星绕地球做匀速圆周运动且运行周期为T,求卫星运行半径r;
(3)由题目所给条件,请提出一种估算地球平均密度的方法,并推导出密度表达式.
(1)求卫星环绕地球运行的第一宇宙速度v1;
(2)若卫星绕地球做匀速圆周运动且运行周期为T,求卫星运行半径r;
(3)由题目所给条件,请提出一种估算地球平均密度的方法,并推导出密度表达式.
分析:(1)第一宇宙速度为卫星在地面附近轨道做匀速圆周运动的环绕速度,根据重力等于向心力列式求解;
(2)根据卫星受到的万有引力等于向心力和地面附近的重力加速度公式联立列式求解;
(3)根据地面附近的重力加速度公式先计算出地球质量,再估算密度.
(2)根据卫星受到的万有引力等于向心力和地面附近的重力加速度公式联立列式求解;
(3)根据地面附近的重力加速度公式先计算出地球质量,再估算密度.
解答:解:(1)重力等于向心力
mg=m
解得
v1=
即卫星环绕地球运行的第一宇宙速度v1为
.
(2)若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即
mg=G
①
卫星受到的万有引力等于向心力
G
=m′
r ②
由①②两式解得
r=
即卫星运行半径r为
.
(3)由①式解得
M=
因而
ρ=
=
=
即地球的密度为
.
mg=m
| ||
| R |
解得
v1=
| gR |
即卫星环绕地球运行的第一宇宙速度v1为
| gR |
(2)若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即
mg=G
| mM |
| R2 |
卫星受到的万有引力等于向心力
G
| m′M |
| r2 |
| 4π2 |
| T2 |
由①②两式解得
r=
| 3 |
| ||
即卫星运行半径r为
| 3 |
| ||
(3)由①式解得
M=
| gR2 |
| G |
因而
ρ=
| M |
| V |
| ||
|
| 3g |
| 4πGR |
即地球的密度为
| 3g |
| 4πGR |
点评:卫星类问题关键抓住引力提供向心力和地面附近重力加速度公式列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
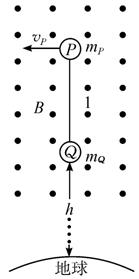
 (2005?北京)近期《科学》中文版的文章介绍了一种新技术--航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统.飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等.从1967年至1999年的17次试验中,飞缆系统试验已获得部分成功.该系统的工作原理可用物理学的基本定律来解释.如图为飞缆系统的简化模型示意图,图中两个物体P、Q的质量分别为mP、mQ,柔性金属缆索长为l,外有绝缘层,系统在近地轨道作圆周运动.运动过程中Q距地面高为h.设缆索总保持指向地心,P的速度为vP.已知地球半径为R,地面的重力加速度为g.
(2005?北京)近期《科学》中文版的文章介绍了一种新技术--航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统.飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等.从1967年至1999年的17次试验中,飞缆系统试验已获得部分成功.该系统的工作原理可用物理学的基本定律来解释.如图为飞缆系统的简化模型示意图,图中两个物体P、Q的质量分别为mP、mQ,柔性金属缆索长为l,外有绝缘层,系统在近地轨道作圆周运动.运动过程中Q距地面高为h.设缆索总保持指向地心,P的速度为vP.已知地球半径为R,地面的重力加速度为g.