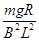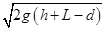题目内容
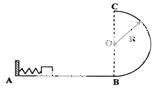
如图所示,在竖直面内有固定轨道ABCDE,其中BC是半径为R的四分之一圆弧轨道,AB(AB>R)是竖直轨道,CE是足够长的水平轨道,CD>R。AB与BC相切于B点,BC与CE相切于C点,轨道的AD段光滑,DE段粗糙且足够长。一根长为R的轻杆两端分别固定有质量均为m的相同小球P、Q(视为质点),将轻杆锁定在图示位置,此位置Q与B等高。现解除锁定释放轻杆,轻杆将沿轨道下滑,Q球经过D点后,沿轨道继续滑行了3R而停下。重力加速度为g。求:
(1)P球到达C点时的速度大小v1;
(2)两小球与DE段轨道间的动摩擦因数 ;
;
(3)Q球到达C点时的速度大小v2。
(1)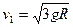 (2)
(2)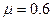 (3)
(3)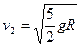
解析试题分析:(1) 从释放到P到达C全过程系统机械能守恒,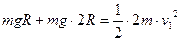 解得:
解得: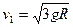
(2)从释放到停下全过程用动能定理,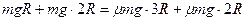 。解得:
。解得: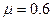
(3):Q到C点时,P离水平轨道的高度为R/2,从释放到此时机械能守恒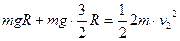 解得:
解得: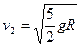
考点:考查了机械能守恒定律以及动能定理的综合应用
点评:关键是把握全过程和分过程中满足的条件,然后根据相应的规律解题

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
物体在做某种运动过程中,重力对物体做功200J,则
| A.物体的动能一定增加200J | B.物体的动能一定减少200J |
| C.物体的重力势能一定减少200J | D.物体的重力势能一定增加200J |
如图所示,小明在玩蹦蹦杆。在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是
| A.重力势能减小,弹性势能增大 |
| B.重力势能增大,弹性势能增大 |
| C.重力势能减小,弹性势能减小 |
| D.重力势能增大,弹性势能减小 |
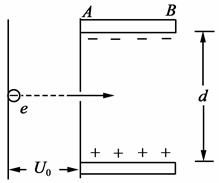
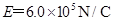 ,方向与x轴正方向相同.在O处放一个电荷量
,方向与x轴正方向相同.在O处放一个电荷量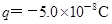 ,质量
,质量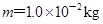 的绝缘物块.物块与水平面间的动摩擦因数
的绝缘物块.物块与水平面间的动摩擦因数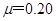 ,沿x轴正方向给物块一个初速度
,沿x轴正方向给物块一个初速度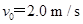 ,如上图所示.(g取
,如上图所示.(g取 )试求:
)试求: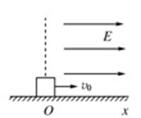
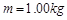 的重物由静止下落,在纸带上打出一系列的
的重物由静止下落,在纸带上打出一系列的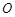 为开始打出的第一点,
为开始打出的第一点,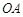 之间有若干点未标出,
之间有若干点未标出,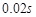 ,重力加速度
,重力加速度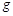 取
取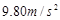 。
。
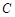 ”)端在上面;
”)端在上面;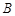 的过程中,动能的变化量△
的过程中,动能的变化量△ (取两位有效数字);
(取两位有效数字);
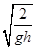 d
d