题目内容
（8分）如图所示，长为l的绝缘细线一端悬于O点，另一端系一质量为m、电荷量为q的小球。现将此装置放在水平向右的匀强电场中，小球静止在A点，此时细线与竖直方向成37°角。重力加速度为g，sin37°=0.6，cos37°=0.8。
（1）判断小球的带电性质；
（2）求该匀强电场的电场强度E的大小；
（3）若将小球向左拉起至与O点处于同一水平高度且细绳刚好张紧，将小球由静止释放，求小球运动到最低点时的速度大小。
【答案】
（1）负电 （2）
（3）
【解析】
试题分析：（1）小球在A点静止，其受力情况如下图所示。根据平衡条件，电场力水平向左与电场线方向相反，判断小球带负电。 （2分）
（2）根据共点力平衡条件有 mgtan37°=qE
解得 （3分）
（3）设小球到达最低点时的速度为v，小球从水平位置运动到最低点的过程中，根据动能定理有：
（2分）
解得：v=
=
（1分）
考点：静电场中的平衡 动能定理
练习册系列答案
相关题目
如图所示，在场强为E的水平匀强电场中，一根长为l的绝缘杆，两端分别固定着带有电量+q和-q的小球（大小不计）．现让缘绝杆绕中点O逆时针转动α角，则转动中带电小球克服电场力做功为
如图所示，圆柱形绝热气缸（设其足够长）固定于水平面上，缸内用绝热活塞密封一定质量的理想气体，已知活塞与气缸壁的接触是光滑的，活塞的横截面积为S，大气压强为P0，电源和电热丝构成回路．可以对气体缓慢加热．开始时，电路未接通，系统处于平衡状态，封闭气体的温度为T1．现用两种方法使气缸内气体温度，均由T1缓慢升高到T2．第一次先将活塞固定，接通电路后电热丝产生的热量为Q1；第二次活塞不固定．可以缓慢自由移动，接通电路后电热丝产生的热量为Q2．
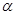角，则转动中带电小球克服电场力做功为___________．