题目内容
三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同均为200N，它们共同悬挂一重物，如图所示，其中OB是水平的，A端、B端固定，θ=30°．则O点悬挂的重物G不能超过（ ）分析：假设细绳OA、OB、OC均不被拉断．以结点O为研究对象，分析受力，作出力图，根据平衡条件比较三绳拉力的大小关系，判断随着重物重力增大，哪根绳拉力先被拉断，再求解最大重力．
解答：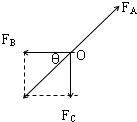
解：假设细绳OA、OB、OC均不被拉断．以结点O为研究对象，分析受力，作出力图如图，由平衡条件得知：
FB与FC的合力与FA大小相等、方向相反，由几何知识得知，细绳OA拉力FA最大，则随着重物重力增大，细绳OA拉力先被拉断，则当细绳OA拉力达到最大时，悬挂的重物G达到最大，
此时最大重力Gmax=FC=FAsinθ=200×
N=100N
故选A
解：假设细绳OA、OB、OC均不被拉断．以结点O为研究对象，分析受力，作出力图如图，由平衡条件得知：FB与FC的合力与FA大小相等、方向相反，由几何知识得知，细绳OA拉力FA最大，则随着重物重力增大，细绳OA拉力先被拉断，则当细绳OA拉力达到最大时，悬挂的重物G达到最大，
此时最大重力Gmax=FC=FAsinθ=200×
| 1 |
| 2 |
故选A
点评：本题采用假设法，通过分析三根绳子拉力大小关系判断哪根先断是关键，同时在正确分析受力情况，作出力图．
练习册系列答案
相关题目
