题目内容
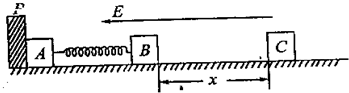
如图所示,在绝缘光滑水平桌面上的左端固定挡板P,小物块A、B、C的质量均为m,A、C带电量均为+q,B不带电,A、B两物块由绝缘的轻弹簧相连接.整个装置处在场强为E,方向水平向左的匀强电场中,开始时A靠在挡板处(但不粘连)且A、B静止,已知弹簧的劲度系数为k,不计AC间库仑力,且带电量保持不变,B、C碰后结合在一起成为一个(设在整个运动过程中,A、B、C保持在一条直线上).(提示:弹簧弹性势能Ep=
kx2,x为形变量)
(1)若在离物块B的x远处由静止释放物块C,可使物块A恰好能离开挡板P,求距离x为多大?
(2)若保持x不变,把物块C的带电量改为+2q,还是由静止释放C,则当物块A刚要离开挡板时,物块B的速度为多大?
| 1 | 2 |
(1)若在离物块B的x远处由静止释放物块C,可使物块A恰好能离开挡板P,求距离x为多大?
(2)若保持x不变,把物块C的带电量改为+2q,还是由静止释放C,则当物块A刚要离开挡板时,物块B的速度为多大?

分析:(1)碰撞前对物体C运用动能定理列式;碰撞过程对BC整体运用动量守恒定律列式;碰撞后直到离开过程运用功能关系列式;A恰好能离开挡板P时电场力和弹簧的拉力平衡;
(2)重复第一问过程列式求解.
(2)重复第一问过程列式求解.
解答:解:(1)由题意知,弹簧原来处于原长,设C碰B前速度为V0,碰后速度为V1
由动能定理有:qEx=
m
由动量守恒有:mv0=2mv1
A恰好能离开挡板时,弹簧对A的拉力F=kx0=qE(xo是弹簧的伸长量)
对BC整体,当A恰好要离开挡板时BC的速度变为零,从碰后的瞬间开始到弹簧伸长的过程中,由能量守恒定律有:
×2m
=
k
+qEx0
由以上式子解得:x=
(2)当物块C的带电量变为2q 时,由动能定理有:2qEx=
m
由动量守恒有:mv0=2mv1
A恰好能离开挡板时,弹簧对A的拉力F=kx0=qE(xo是弹簧的伸长量)
对BC整体,当A恰好要离开挡板时BC的速度为v,从碰后的瞬间开始到弹簧伸长的过程中,由能量守恒定律有:
×2m
=
k
+2qEx0+
?2mv2,解得:v=Eq
答:(1)距离x为
;
(2)物块B的速度为Eq
.
由动能定理有:qEx=
| 1 |
| 2 |
| v | 2 0 |
由动量守恒有:mv0=2mv1
A恰好能离开挡板时,弹簧对A的拉力F=kx0=qE(xo是弹簧的伸长量)
对BC整体,当A恰好要离开挡板时BC的速度变为零,从碰后的瞬间开始到弹簧伸长的过程中,由能量守恒定律有:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| x | 2 0 |
由以上式子解得:x=
| 3qE |
| k |
(2)当物块C的带电量变为2q 时,由动能定理有:2qEx=
| 1 |
| 2 |
| v | 2 0 |
由动量守恒有:mv0=2mv1
A恰好能离开挡板时,弹簧对A的拉力F=kx0=qE(xo是弹簧的伸长量)
对BC整体,当A恰好要离开挡板时BC的速度为v,从碰后的瞬间开始到弹簧伸长的过程中,由能量守恒定律有:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| 2 |
|
答:(1)距离x为
| 3qE |
| k |
(2)物块B的速度为Eq
|
点评:本题要灵活地选择研究对象、研究过程运用动能定理、功能关系、动量守恒定律列式求解,弄清运动过程是关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图所示,在绝缘光滑水平面上,有一个边长为L的单匝正方形线框abcd,在外力的作用下以恒定的速率v向右运动进入磁感应强度为B的有界匀强磁场区域.线框被全部拉入磁场的过程中线框平面保持与磁场方向垂直,线框的ab边始终平行于磁场的边界.已知线框的四个边的电阻值相等,均为R.求:
如图所示,在绝缘光滑水平面上,有一个边长为L的单匝正方形线框abcd,在外力的作用下以恒定的速率v向右运动进入磁感应强度为B的有界匀强磁场区域.线框被全部拉入磁场的过程中线框平面保持与磁场方向垂直,线框的ab边始终平行于磁场的边界.已知线框的四个边的电阻值相等,均为R.求: 如图所示,在绝缘光滑的水平面上固定两个带有等量同种电荷的小球P、Q,在PQ之间的M点由静止释放一带电滑块,则滑块会由静止开始向右运动到PQ之间的另一点N而速度减为零,在此过程中,以下说法正确的是( )
如图所示,在绝缘光滑的水平面上固定两个带有等量同种电荷的小球P、Q,在PQ之间的M点由静止释放一带电滑块,则滑块会由静止开始向右运动到PQ之间的另一点N而速度减为零,在此过程中,以下说法正确的是( )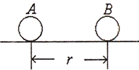 如图所示,在绝缘光滑水平面上,可视为质点的A、B两个带正电的小球相距为r,带电量分别为4q和q.B的质量为m,在库仑力作用下,两球从静止开始运动:起初,A的加速度大小为a、B的加速度大小为4a;经过一段时间后,B的加速度大小为a,速度达到v.试计算这时:
如图所示,在绝缘光滑水平面上,可视为质点的A、B两个带正电的小球相距为r,带电量分别为4q和q.B的质量为m,在库仑力作用下,两球从静止开始运动:起初,A的加速度大小为a、B的加速度大小为4a;经过一段时间后,B的加速度大小为a,速度达到v.试计算这时: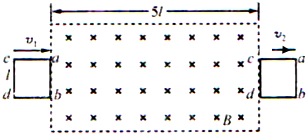 如图所示,在绝缘光滑的水平面上,有一个质量为m、边长为L的正方形线框,用一垂直于ab 边的恒定外力将正方形线框以速率v1匀速拉进磁感应强度为B的有界匀强磁场区域,当正方形线框全部进入磁场后立即将外力撤去,线框最终能完全离开磁场,若测得cd边刚要离开磁场时速率为v2,已知磁场方向竖直向下,宽度为5L,正方形线框每条边的电阻均为R,求:
如图所示,在绝缘光滑的水平面上,有一个质量为m、边长为L的正方形线框,用一垂直于ab 边的恒定外力将正方形线框以速率v1匀速拉进磁感应强度为B的有界匀强磁场区域,当正方形线框全部进入磁场后立即将外力撤去,线框最终能完全离开磁场,若测得cd边刚要离开磁场时速率为v2,已知磁场方向竖直向下,宽度为5L,正方形线框每条边的电阻均为R,求: (2011?浙江模拟)如图所示,在绝缘光滑的水平面上固定两个电量相等的异种点电荷A、B,其中A带正电,B带负电荷,它们的连线的中点是O,MN是AB在水平面内中垂线上的两点.空间中还有一个垂直于该水平面的磁场(图中未画出).现有一个带电量为+q的小球以初速度v0从M点沿MN方向射入,恰能沿中垂线由M点向N点运动,则下列说法中正确的是( )
(2011?浙江模拟)如图所示,在绝缘光滑的水平面上固定两个电量相等的异种点电荷A、B,其中A带正电,B带负电荷,它们的连线的中点是O,MN是AB在水平面内中垂线上的两点.空间中还有一个垂直于该水平面的磁场(图中未画出).现有一个带电量为+q的小球以初速度v0从M点沿MN方向射入,恰能沿中垂线由M点向N点运动,则下列说法中正确的是( )