题目内容
16. 光滑水平面上有一质量为M的滑块,滑块的左侧是一光滑的$\frac{1}{4}$圆弧,圆弧半径为R=1m.一质量为m的小球以速度v0向右运动冲上滑块.已知M=4m.g取10m/s2,若小球刚好没跃出$\frac{1}{4}$圆弧的上端.全过程机械能不损失.求:
光滑水平面上有一质量为M的滑块,滑块的左侧是一光滑的$\frac{1}{4}$圆弧,圆弧半径为R=1m.一质量为m的小球以速度v0向右运动冲上滑块.已知M=4m.g取10m/s2,若小球刚好没跃出$\frac{1}{4}$圆弧的上端.全过程机械能不损失.求:(1)小球的初速度v0;
(2)滑块获得的最大速度.
分析 (1)小球刚好没跃出圆弧的上端,知小球上升到滑块上端时,小球与滑块水平方向速度相同,结合动量守恒和系统机械能守恒求出小球的初速度大小.
(2)小球到达最高点以后又滑回,滑块又做加速运动,当小球离开滑块后滑块速度最大,根据动量守恒和能量守恒求出滑块的最大速度.
解答 解:(1)当小球上升到滑块上端时,小球与滑块水平方向速度相同,设为v1,以小球的初速度方向为正方向,在水平方向上,由动量守恒定律得:
mv0=(m+M)v1…①
由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$(m+M)v12+mgR …②,
代入数据解得:v0=5m/s …③;
(2)小球到达最高点以后又滑回,滑块又做加速运动,当小球离开滑块后滑块速度最大.研究小球开始冲上滑块一直到离开滑块的过程,以小球的初速度方向为正方向,由动量守恒定律得:
mv0=mv2+Mv3…④
由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv22+$\frac{1}{2}$Mv32…⑤
解得:v3=$\frac{2m}{m+M}$v0=2m/s…⑥
答:(1)小球的初速度v0是5m/s.
(2)滑块获得的最大速度是2m/s.
点评 本题考查了动量守恒定律、机械能守恒定律以及能量守恒定律等,知道小球刚好没跃出圆弧的上端,两者水平方向上的速度相同;当小球返回离开滑块时,滑块的速度最大.

练习册系列答案
相关题目
13. 如图所示,三个带正电粒子,以相同速度从带电平行金属板间的P点沿垂直于电场方向射入电场,落在A、B、C三点,粒子重力不计,下列说法中正确的是( )
如图所示,三个带正电粒子,以相同速度从带电平行金属板间的P点沿垂直于电场方向射入电场,落在A、B、C三点,粒子重力不计,下列说法中正确的是( )
 如图所示,三个带正电粒子,以相同速度从带电平行金属板间的P点沿垂直于电场方向射入电场,落在A、B、C三点,粒子重力不计,下列说法中正确的是( )
如图所示,三个带正电粒子,以相同速度从带电平行金属板间的P点沿垂直于电场方向射入电场,落在A、B、C三点,粒子重力不计,下列说法中正确的是( )| A. | 三粒子在电场中运动的时间相等 | |
| B. | 三粒子的电荷时关系是qA>qB>qC | |
| C. | 三粒子在电场中的加速度关系是ac>aB>aA | |
| D. | 三粒子到达极板的速度大小关系是υC>υB>υA |
14.人造地球卫星绕地球做匀速圆周运动,离地面越远的卫星( )
| A. | 向心加速度越大 | B. | 线速度越大 | C. | 角速度越大 | D. | 周期越大 |
4.把一个物体在高为h处以初速度v0水平抛出,若落地时速度为v,它的垂直分速度为vy,则不能用来计算物体在空中运动时间的是( )
| A. | $\frac{{v}_{y}-{v}_{0}}{g}$ | B. | $\sqrt{\frac{2h}{g}}$ | C. | $\frac{\sqrt{{v}^{2}{-v}_{0}^{2}}}{g}$ | D. | $\frac{2h}{{v}_{y}}$ |
8.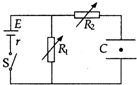 如图所示,电路中R1、R2均为可变电阻,电源电动势为E,内阻为r,平行板电容器C的极板水平放置,闭合开关S,电路达到稳定时,有一带电油滴恰好悬浮在两极板之间静止不动,如果仅改变下列某一个条件,能使油滴向下运动的是( )
如图所示,电路中R1、R2均为可变电阻,电源电动势为E,内阻为r,平行板电容器C的极板水平放置,闭合开关S,电路达到稳定时,有一带电油滴恰好悬浮在两极板之间静止不动,如果仅改变下列某一个条件,能使油滴向下运动的是( )
 如图所示,电路中R1、R2均为可变电阻,电源电动势为E,内阻为r,平行板电容器C的极板水平放置,闭合开关S,电路达到稳定时,有一带电油滴恰好悬浮在两极板之间静止不动,如果仅改变下列某一个条件,能使油滴向下运动的是( )
如图所示,电路中R1、R2均为可变电阻,电源电动势为E,内阻为r,平行板电容器C的极板水平放置,闭合开关S,电路达到稳定时,有一带电油滴恰好悬浮在两极板之间静止不动,如果仅改变下列某一个条件,能使油滴向下运动的是( )| A. | 减小R2的阻值 | B. | 减小R1的阻值 | ||
| C. | 增大两极板间的距离 | D. | 减小两极板间的正对面积 |
5.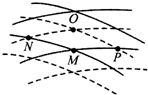 如图所示,实线与虚线分别表示振幅、频率均相同的两列水波的波峰和波谷,此刻,M是两列波的波峰与波峰的相遇点,下列说法中正确的是( )
如图所示,实线与虚线分别表示振幅、频率均相同的两列水波的波峰和波谷,此刻,M是两列波的波峰与波峰的相遇点,下列说法中正确的是( )
 如图所示,实线与虚线分别表示振幅、频率均相同的两列水波的波峰和波谷,此刻,M是两列波的波峰与波峰的相遇点,下列说法中正确的是( )
如图所示,实线与虚线分别表示振幅、频率均相同的两列水波的波峰和波谷,此刻,M是两列波的波峰与波峰的相遇点,下列说法中正确的是( )| A. | 质点P始终处于平衡位置 | |
| B. | O、M两质点始终处在最大位移处 | |
| C. | 从该时刻起,经过四分之一周期,质点O到达平衡位置 | |
| D. | 随着时间的推移,质点M将向O点处移动 |
6.用m表示地球的同步卫星的质量,h表示它离地面的高度,R0表示地球的半径,g0表示地球表面的重力加速度,ω0为地球自转的角速度,则该卫星所受地球的万有引力为F,则( )
| A. | F=$\frac{GMm}{({R}_{0}+h)^{2}}$ | B. | F=mω02R0 | ||
| C. | F=$\frac{m{g}_{0}{R}_{0}^{2}}{({R}_{0}+h)^{2}}$ | D. | 轨道平面不一定与赤道平面重合 |



