��Ŀ����
�ڡ���֤��е���غ㶨�ɡ�ʵ���У�����ʱ�����ڵ�ѹΪU��Ƶ��Ϊf�Ľ�����Դ�ϣ���ʵ���д���һ��������ֽ������ͼ��ʾ��ѡȡֽ���ϴ��������5����A��B��C��D��E�����A������ʼ��O�ľ���Ϊs0��A��C�����ľ���Ϊs1��C��E�����ľ���Ϊs2������ش�������Ϊm����֪���ص��������ٶ�Ϊg����Ӵ�����ʼ��O������C��Ĺ����У��ش��������ܵļ�������EP= ���ش����ܵ���������Ek= ���ش�����ļ��ٶ�a= ��


������ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȣ��Ӷ�������ܣ�
���ݹ��ܹ�ϵ���������ܼ�С������������������ֵ��
�ɡ�x=aT2�����ٶȣ�
���ݹ��ܹ�ϵ���������ܼ�С������������������ֵ��
�ɡ�x=aT2�����ٶȣ�
����⣺�ش��������ܵļ�����Ϊ��EP=mg��s0+s1����
��C���ش����ٶ�vC=
=
��
T=2��
�ش����ܵ�������Ϊ��Ek=
�ɡ�x=aT2�ã�
s2-s1=aT2��
a=
�ʴ�Ϊ��mg��s0+s1����
��
��C���ش����ٶ�vC=
| XAE |
| tAE |
| s1+s2 |
| 2T |
T=2��
| 1 |
| f |
�ش����ܵ�������Ϊ��Ek=
| m(s1+s2)2f2 |
| 32 |
�ɡ�x=aT2�ã�
s2-s1=aT2��
a=
| f2(s2-s1) |
| 4 |
�ʴ�Ϊ��mg��s0+s1����
| m(s1+s2)2f2 |
| 32 |
| f2(s2-s1) |
| 4 |
�������������׳����ĵط���T=
��Ҫע�����ֵ�Դ�������������ʱ������ʽ�С�x=aT2��T�Ǽ�����ʱ������
| 1 |
| f |

��ϰ��ϵ�д�
 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
�����Ŀ
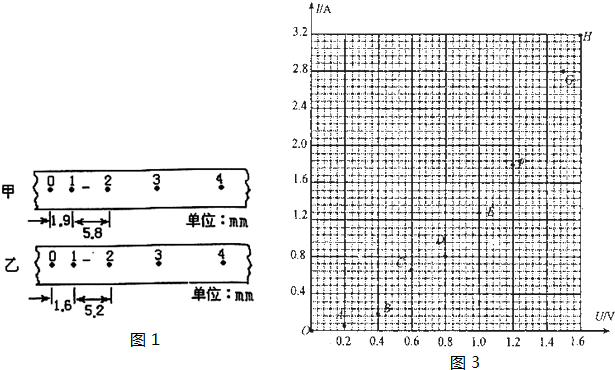
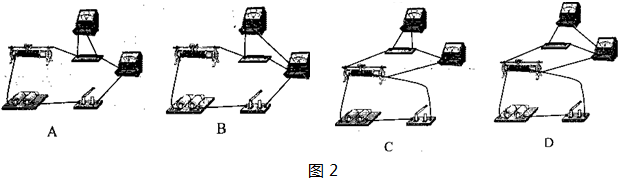
 ��2010?�ɶ���ģ����1������֤����е���غ㶨�ʡ��������У�
��2010?�ɶ���ģ����1������֤����е���غ㶨�ʡ��������У�
