题目内容
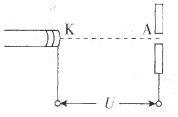
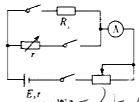
【题目】如图所示,粗糙水平面上静止放置一质量为2m的木板,在木板上右端静置一质量为m的小滑块。一可视为质点、质量为2m的小朋友荡秋千,从A点由静止出发绕O点下摆,当摆到最低点B时,小朋友在极短时间内用脚水平蹬踏木板的左端,然后自己刚好能回到A点。已知秋千的摆绳长为L,质量不计,AO与竖直方向的夹角为60°。小滑块与木板之间、木板与水平面间的动摩擦因数都是![]() ,重力加速度为g。求:
,重力加速度为g。求:
(1)秋千摆到最低点B,小朋友未蹬踏木板时秋干摆绳的拉力大小;
(2)小朋友蹬踏木板过程中,小朋友做功大小;
(3)若小滑块不从木板上滑下,木板至少应为多长。

【答案】(1)4mg (2)![]() (3)
(3)![]()
【解析】
(1)从A点下摆到B点,只有重力做功,机械能守恒。由机械能守恒定律求出小朋友运动到最低点时的速度。在最低点,由合力充当向心力,由向心力公式求解秋千绳的拉力;(2)小朋友蹬踏木板过程中,沿水平方向动量守恒。由动量守恒定律列式。再由动能定理求小朋友做功大小;(3)由牛顿第二定律分别求出滑块和木板的加速度,结合运动学公式可求得木板的长度.
(1)小朋友从A点下摆到B点,只有重力做功,机械能守恒.
设到达B点的速度大小为v0,则由机械能守恒定律有:![]()
绳子拉力设为T,由受力分析和圆周运动知识有:![]()
解得:T=4mg
(2)由题意知,小朋友蹬踏木板后速度大小不变,方向向左
由动量守恒定律得:2mv0=-2mv0+2mv1
得木板的速度:![]()
小朋友做功大小:![]()
(3)由牛顿第二定律得:小滑块的加速度:![]()
木板的加速度:![]()
当二者速度相等后,由于整体的加速度等于滑块的最大加速度,所以此后二者保持相对静止,设此过程经过的时间为t
由速度关系得:v1-a板t=a块t
此过程木板的位移:![]()
滑块的位移:![]()
小滑块不从木板上滑下,木板至少应为:x=x板-x块
解得:![]()