题目内容
 如图,半径为R=10cm的光滑大圆环竖直放置,轻质弹簧的一端固定在圆环上的A点,A点与圆心O在同一高度,另一端与小球B相连,B球穿在大圆环上.当弹簧与水平线OA成370角时,小球B恰处于平衡状态.已知小球B的重力为15N,弹簧的劲度系数为350N/m,求:
如图,半径为R=10cm的光滑大圆环竖直放置,轻质弹簧的一端固定在圆环上的A点,A点与圆心O在同一高度,另一端与小球B相连,B球穿在大圆环上.当弹簧与水平线OA成370角时,小球B恰处于平衡状态.已知小球B的重力为15N,弹簧的劲度系数为350N/m,求:(1)平衡时,轻弹簧AB的长度为多少cm,此时弹簧比原长长还是短?
(2)轻弹簧的原长为多少cm?
分析:(1)根据几何知识求出平衡时轻弹簧AB的长度.由小球的受力情况,分析弹簧的状态,判断此时弹簧与原长的大小关系.
(2)以小球B为研究对象,分析受力情况,根据三角形相似法求解弹簧的弹力,由胡克定律求出原长.
(2)以小球B为研究对象,分析受力情况,根据三角形相似法求解弹簧的弹力,由胡克定律求出原长.
解答:解:(1)平衡时,根据几何知识得,弹簧长度为L=2Rcos37°=16cm.由小球的受力情况可知,弹簧对小球施加的是压力,说明弹簧处于压缩状态,
此时弹簧比原长短.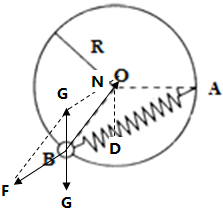
(2)以小球B为研究对象,分析受力情况,作出相似三角形,则得
=
又BD=L-
=3.5cm
代入解得弹力为F=7N,
则原长为L0=
+L=
m+16cm=18cm
答:
(1)平衡时,轻弹簧AB的长度为16cm,此时弹簧比原长短.
(2)轻弹簧的原长为18cm.
此时弹簧比原长短.

(2)以小球B为研究对象,分析受力情况,作出相似三角形,则得
| F |
| BD |
| G |
| Rtan37° |
又BD=L-
| R |
| cos37° |
代入解得弹力为F=7N,
则原长为L0=
| F |
| k |
| 7 |
| 350 |
答:
(1)平衡时,轻弹簧AB的长度为16cm,此时弹簧比原长短.
(2)轻弹簧的原长为18cm.
点评:本题运用三角形相似法研究非直角三角形的力平衡问题,是常用的方法,也可以运用三角函数法求解.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 如图所示,ABC为固定在竖直面内的光滑四分之一圆轨道,其半径为r=10m,N为固定在水平面内的半圆平面,其半径为R=
如图所示,ABC为固定在竖直面内的光滑四分之一圆轨道,其半径为r=10m,N为固定在水平面内的半圆平面,其半径为R=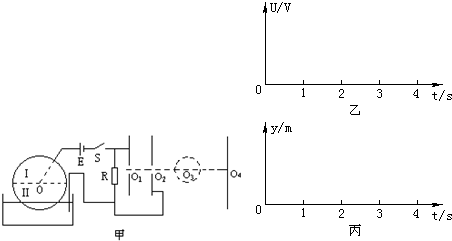 如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
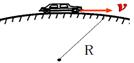
如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的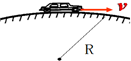 如图,汽车以某一速度通过半径为R=10米的拱桥最高点时,汽车对对拱桥的压力恰好为零.则汽车此时的速度为
如图,汽车以某一速度通过半径为R=10米的拱桥最高点时,汽车对对拱桥的压力恰好为零.则汽车此时的速度为