题目内容
13.某公路同一直线车道上同向匀速行驶着轿车和货车,货车额定功率为90kW,质量为2×103kg,行驶中阻力恒为f=1×103N,速度为v1=30m/s,而轿车以v2=40m/s运动,在距货车s0=100m时发现前方有货车,在轿车不改变速度的情况下只是给货车发信号让其加速运动,货车司机瞬间听到信号开始以加速度a=0.5m/s2加速运动,两车可视为质点,试通过计算分析轿车是否会在货车匀加速运动阶段撞上货车?分析 轿车恰好撞不上货车的临界条件为追及时两车的速度相同.由货车额定功率为90kW,质量为2×103kg,行驶中阻力恒为f=1×105N,速度为v1=30m/s可以得到货车匀加速阶段的最大速度,及达到最大速度的时间,列方程讨论即可.
解答 解:匀加速阶段的货车的牵引力为:F=f+ma=1×103+2×103×0.5N=2×103N…①
设匀加速阶段的最大速度为vm,则有,P=Fvm…②
匀加速的时间为:t=$\frac{{v}_{m}{-v}_{1}}{a}$…③
联立①②③得,t=30s,vm=45m/s
货车加速到40m/s的时间为:t′=$\frac{{v}_{2}{-v}_{1}}{a}=\frac{40-30}{0.5}s=20s$
货车在20s时间内的位移为:x=$\frac{{v}_{1}{+v}_{2}}{2}×t′=\frac{30+40}{2}×20m=700m$
此段时间内轿车的位移为:x′=v2t′=40×20m=800m
由于x′-x=100m=s0=100m
故轿车恰好不会在货车匀加速运动阶段撞上货车.
答:轿车恰好不会在货车匀加速运动阶段撞上货车.
点评 关键知道恰好撞不上货车的临界条件为追及时两车的速度相同,能够利用牛顿第二定律结合功率的计算公式求解匀加速阶段的末速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.根据分子动理论判断以下关于分子力和分子势能的说法中正确的是( )
| A. | 当分子间距离为平衡距离r0时,分子具有最大势能 | |
| B. | 当分子间距离为平衡距离r0时,分子具有最小势能 | |
| C. | 当分子间距离为平衡距离r0时,引力和斥力都是最大值 | |
| D. | 当分子间距离为平衡距离r0时,引力和斥力都是零 |
1.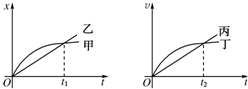 如图所示的位移x-t图象和速度v-t图象中,给出的四条图线甲、乙、丙、丁分别代表四辆车由同一地点向同一方向运动的情况,则下列说法正确的是( )
如图所示的位移x-t图象和速度v-t图象中,给出的四条图线甲、乙、丙、丁分别代表四辆车由同一地点向同一方向运动的情况,则下列说法正确的是( )
 如图所示的位移x-t图象和速度v-t图象中,给出的四条图线甲、乙、丙、丁分别代表四辆车由同一地点向同一方向运动的情况,则下列说法正确的是( )
如图所示的位移x-t图象和速度v-t图象中,给出的四条图线甲、乙、丙、丁分别代表四辆车由同一地点向同一方向运动的情况,则下列说法正确的是( )| A. | 甲车做直线运动,乙车做曲线运动 | |
| B. | 0~t1时间内,甲车通过的路程大于乙车通过的路程 | |
| C. | 0~t2时间内,丙、丁两车在t2时刻相距最远 | |
| D. | 0~t2时间内,丙、丁两车的平均速度相等 |
8.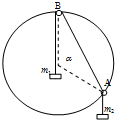 如图所示,小圆环A吊着一个质量为m2的物块并套在竖直放置的大圆环上.另有一根细绳,一端拴着质量为m1的物块,跨过固定在大圆环最高点B处的小定滑轮后,另一端系在小圆环A上.设小圆环、滑轮、绳子的质量以及相互之间的摩擦均不计,绳子不可伸长.若平衡时弦AB所对应的圆心角为α,则两物块的质量比m1:m2为( )
如图所示,小圆环A吊着一个质量为m2的物块并套在竖直放置的大圆环上.另有一根细绳,一端拴着质量为m1的物块,跨过固定在大圆环最高点B处的小定滑轮后,另一端系在小圆环A上.设小圆环、滑轮、绳子的质量以及相互之间的摩擦均不计,绳子不可伸长.若平衡时弦AB所对应的圆心角为α,则两物块的质量比m1:m2为( )
 如图所示,小圆环A吊着一个质量为m2的物块并套在竖直放置的大圆环上.另有一根细绳,一端拴着质量为m1的物块,跨过固定在大圆环最高点B处的小定滑轮后,另一端系在小圆环A上.设小圆环、滑轮、绳子的质量以及相互之间的摩擦均不计,绳子不可伸长.若平衡时弦AB所对应的圆心角为α,则两物块的质量比m1:m2为( )
如图所示,小圆环A吊着一个质量为m2的物块并套在竖直放置的大圆环上.另有一根细绳,一端拴着质量为m1的物块,跨过固定在大圆环最高点B处的小定滑轮后,另一端系在小圆环A上.设小圆环、滑轮、绳子的质量以及相互之间的摩擦均不计,绳子不可伸长.若平衡时弦AB所对应的圆心角为α,则两物块的质量比m1:m2为( )| A. | cos$\frac{α}{2}$ | B. | 2sin$\frac{α}{2}$ | C. | sin$\frac{α}{2}$ | D. | 2cos$\frac{α}{2}$ |
5.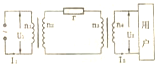 如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )
如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )
 如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )
如图所示,远距离输电线路中,升压变压器和降压变压器均为理想变压器,且$\frac{{n}_{2}}{{n}_{1}}$=$\frac{{n}_{3}}{{n}_{4}}$.升压变压器原线圈的电压为U1,原线圈中电流为I1;降压变压器副线圈的电压为U2,副线圈中电流为I2.远距离输电线路上电阻的电压为U额.则下列说法正确的是( )| A. | U额=U1-U2 | B. | U额>U1-U2 | C. | I1=I2 | D. | I1>I2 |
3.下列说法正确的是( )
| A. | 只要知道水的摩尔质量和水分子的质量,就可以计算出阿伏伽德罗常数 | |
| B. | 扩散现象和布朗运动都与温度有关,所以扩散现象和布朗运动都是分子的热运动 | |
| C. | 彩色液晶显示器利用了液晶的光学性质具有各向异性的特点 | |
| D. | 气体对容器的压强是大量气体分子对容器的碰撞引起的,它跟气体分子的密集程度以及气体分子的平均动能有关 |