题目内容
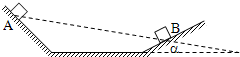 为测量物体与接触面间的动摩擦因数,某同学设计了如图所示的实验.将一带正电物体从斜面的A处由静止开始滑下,经过一水平面后又滑上右边的斜面并停留在B处,若物体与接触面的动摩擦因数处处相等,斜面与水平面接触处是小圆弧,已量得AB连线与水平面成α角,则物体与接触面间的动摩擦因数μ=
为测量物体与接触面间的动摩擦因数,某同学设计了如图所示的实验.将一带正电物体从斜面的A处由静止开始滑下,经过一水平面后又滑上右边的斜面并停留在B处,若物体与接触面的动摩擦因数处处相等,斜面与水平面接触处是小圆弧,已量得AB连线与水平面成α角,则物体与接触面间的动摩擦因数μ=分析:应用动能定理列方程,可以求出动摩擦因素,然后分析答题.
解答:解:设斜面倾角为θ,斜面长为L,物体在斜面上下滑过程中克服阻力做的功为:
W=μmgcosθ.L=μmgL水平,△h=Lsinθ,
则全过程由动能定理应有mg△h-W=0,
即mgLsinθ-μmgLcosθ=0,解得:μ=tanθ;
AB连线与水平面成α角,由动能定理得:mgABsinα-μmgABcosα=0,解得:μ=tanα,
加入竖直向下的电场后,AC连线与水平面夹角为β,
由动能定理得:(mg+qE)ACsinβ-μ(mg+qE)ACcosβ=0,解得μ=tanβ,
μ=tanα,μ=tanβ,μ不变,因此β=α;
故答案为:
故答案为:等于.(共(4分),空2分) tanα等于
W=μmgcosθ.L=μmgL水平,△h=Lsinθ,
则全过程由动能定理应有mg△h-W=0,
即mgLsinθ-μmgLcosθ=0,解得:μ=tanθ;
AB连线与水平面成α角,由动能定理得:mgABsinα-μmgABcosα=0,解得:μ=tanα,
加入竖直向下的电场后,AC连线与水平面夹角为β,
由动能定理得:(mg+qE)ACsinβ-μ(mg+qE)ACcosβ=0,解得μ=tanβ,
μ=tanα,μ=tanβ,μ不变,因此β=α;
故答案为:
故答案为:等于.(共(4分),空2分) tanα等于
点评:掌握斜面上运动过程中摩擦力做功的特点,对多运动过程应用全过程动能定理解决.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 (2011?武汉模拟)卫星绕地球做匀速圆周运动时处于完全失重状态,在这种环境中无法用天平称量物体的质量.于是某同学在这种环境设计了如图所示的装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设航天器中具有基本测量工具.
(2011?武汉模拟)卫星绕地球做匀速圆周运动时处于完全失重状态,在这种环境中无法用天平称量物体的质量.于是某同学在这种环境设计了如图所示的装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设航天器中具有基本测量工具.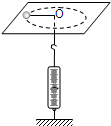 随着航天技术的发展,许多实验可以搬到太空中进行.飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设飞船中具有基本测量工具.
随着航天技术的发展,许多实验可以搬到太空中进行.飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设飞船中具有基本测量工具. 为测量物体与接触面间的动摩擦因数,某同学设计了如图所示的实验.将一带正电物体从斜面的A处由静止开始滑下,经过一水平面后又滑上右边的斜面并停留在B处,若物体与接触面的动摩擦因数处处相等,斜面与水平面接触处是小圆弧,已量得AB连线与水平面成α角,则物体与接触面间的动摩擦因数μ=________.若在整个空间加上竖直向下的电场,则该物体从A点由静止滑下,到达右边的斜面并停留在C处(图中未标出),AC连线与水平面夹角为β,则α、β的关系是α________β(选填“大于”、“小于”或“等于”).
为测量物体与接触面间的动摩擦因数,某同学设计了如图所示的实验.将一带正电物体从斜面的A处由静止开始滑下,经过一水平面后又滑上右边的斜面并停留在B处,若物体与接触面的动摩擦因数处处相等,斜面与水平面接触处是小圆弧,已量得AB连线与水平面成α角,则物体与接触面间的动摩擦因数μ=________.若在整个空间加上竖直向下的电场,则该物体从A点由静止滑下,到达右边的斜面并停留在C处(图中未标出),AC连线与水平面夹角为β,则α、β的关系是α________β(选填“大于”、“小于”或“等于”).