题目内容
在O点固定一个长度为L的轻质不可伸长的细绳,绳子的另一端连接一个质量为m的小球,当绳子与竖直方向为 时,小球以
时,小球以 的垂直于绳子的速度在A点释放,它绕O点在竖直面内做圆周运动,重力加速度为g,求:
的垂直于绳子的速度在A点释放,它绕O点在竖直面内做圆周运动,重力加速度为g,求:

(1)小球到最低点B点时速度大小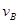
(2)小球到最低点B点时,绳子的拉力F1
(3)小球到最高点c时,绳子的拉力F2
 时,小球以
时,小球以 的垂直于绳子的速度在A点释放,它绕O点在竖直面内做圆周运动,重力加速度为g,求:
的垂直于绳子的速度在A点释放,它绕O点在竖直面内做圆周运动,重力加速度为g,求:
(1)小球到最低点B点时速度大小
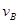
(2)小球到最低点B点时,绳子的拉力F1
(3)小球到最高点c时,绳子的拉力F2
(1)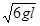 (2) 7mg (3)mg
(2) 7mg (3)mg
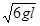 (2) 7mg (3)mg
(2) 7mg (3)mg试题分析:(1)拉力垂直速度方向,不做功,所以过程中只有重力做功,故
 ,解得:
,解得: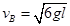
(2)在B点绳子的拉力和重力充当向心力,根据牛顿第二定律可得:
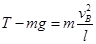 解得:
解得: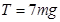
(3)运动过程中,只有重力做功,机械能守恒,所以
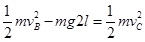 ,根据牛顿第二定律可得:
,根据牛顿第二定律可得: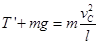 ,解得:
,解得: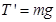
点评:做本题的关键是分析清楚小球做圆周运动是的向心力来源,然后根据牛顿第二定律分析

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
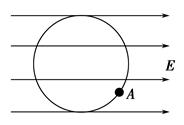

 匀速转动,转台上有一个质量为m的物体,物体与转台间用长L的绳连接着,此时物体与转台处于相对静止,设物体与转台间的动摩擦因数为
匀速转动,转台上有一个质量为m的物体,物体与转台间用长L的绳连接着,此时物体与转台处于相对静止,设物体与转台间的动摩擦因数为 ,现突然制动转台,则
,现突然制动转台,则 
 L
L 圈后,停止运动
圈后,停止运动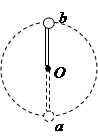
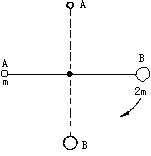

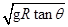 的速度转弯时,则内外轨都不会受到火车轮的侧压力,此时铁轨对火车的支持力为N ,那么
的速度转弯时,则内外轨都不会受到火车轮的侧压力,此时铁轨对火车的支持力为N ,那么