��Ŀ����
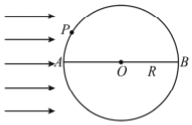
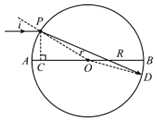
����Ŀ����������е�Բ���β����ĺ������ͼ��ʾ��ABΪˮƽֱ��������ש�İ뾶ΪR��OΪԲ�ģ�PΪԲ���β���ש�ϵ�һ�㣬��ˮƽֱ��AB���![]() ����ɫ��ƽ����ˮƽֱ��AB����ò���ש����֪��ֱ��AB����ĵ�ɫ����������ʱ��Ϊt����������еĴ����ٶ�Ϊc�������Ƕ��η��䣬��
����ɫ��ƽ����ˮƽֱ��AB����ò���ש����֪��ֱ��AB����ĵ�ɫ����������ʱ��Ϊt����������еĴ����ٶ�Ϊc�������Ƕ��η��䣬��
��1����Բ���β���ש��������n��
��2����P��ˮƽ����ĵ�ɫ��������ש��ʱ�䡣
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
��1����AB����Ĺ⽫��B�����������ڲ����ڵ��ٶ�Ϊv����
v��![]()
�֣�
2R��ct
�����ɵã�
n��![]()
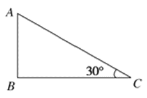
��2����P�������ķ��ߣ���P��AB�Ĵ��ߣ�����ΪC����ͼ����![]() �����ԡ�POC��30��
�����ԡ�POC��30��
�ɼ��ι�ϵ��֪�ù�������Ϊ30��
�����䶨�ɣ�n��![]() �ɵã�
�ɵã�
![]()
�ɼ��ι�ϵ��
PD��2Rcosr
��P����Ĺ��D���õ�ʱ�䣺
![]()
�����ɵã�
t����![]()

��ϰ��ϵ�д�
 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�
�����Ŀ