题目内容
如下图所示,斜面体固定在水平面上,斜面光滑,倾角为θ,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个细物块。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力(k>1),断开轻绳,木板和物块沿斜面下滑。假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计。求:
(1)木板第一次与挡板碰撞弹起上升过程中,物块的加速度;
(2)从断开轻绳到木板与挡板第二次碰撞的瞬间,木板运动的路程s;
(3)从断开轻绳到木板和物块都静止,摩擦力对木板及物块做的总功W。
(1)木板第一次与挡板碰撞弹起上升过程中,物块的加速度;
(2)从断开轻绳到木板与挡板第二次碰撞的瞬间,木板运动的路程s;
(3)从断开轻绳到木板和物块都静止,摩擦力对木板及物块做的总功W。

解:(1)设木板第一次上升过程中,物块的加速度为a物块物块受合力F物块=kmgsinθ-mgsinθ①
由牛顿第二定律F物块=ma物块②
由①②得a物块=(k-1)gsinθ,方向沿斜面向上
(2)设以地面为零势能面,木板第一次与挡板碰撞时的速度大小为v1由机械能守恒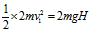
解得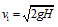
设木板弹起后的加速度a板,由牛顿第二定律a板=-(k+1)gsinθ
S板第一次弹起的最大路程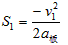
解得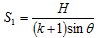
木板运动的路程S=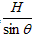 +2S1=
+2S1=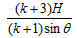
(3)设物块相对木板滑动距离为L 根据能量守恒mgH+mg(H+Lsinθ)=kmgsinθL
摩擦力对木板及物块做的总功W=-kmgsinθL
解得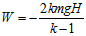 ,负号说明摩擦力对木板及物块做负功。
,负号说明摩擦力对木板及物块做负功。

练习册系列答案
相关题目
 如图所示,斜面体固定在水平面上,质量为m的物体沿斜面匀速下滑,则物体由斜面顶端下滑到斜面底端的过程中,下列叙述正确的是( )
如图所示,斜面体固定在水平面上,质量为m的物体沿斜面匀速下滑,则物体由斜面顶端下滑到斜面底端的过程中,下列叙述正确的是( ) 如图所示,斜面体固定在水平地面上.用一根轻绳跨过定滑轮连接甲、乙两滑块,使其静止于两斜面等高处,轻绳均与斜面平行.甲、乙可看成质点,不计一切摩擦.若剪断轻绳(sin37°=0.6,sin53°=0.8),则( )
如图所示,斜面体固定在水平地面上.用一根轻绳跨过定滑轮连接甲、乙两滑块,使其静止于两斜面等高处,轻绳均与斜面平行.甲、乙可看成质点,不计一切摩擦.若剪断轻绳(sin37°=0.6,sin53°=0.8),则( ) 如图所示,斜面体固定在水平面上,小物块A与斜面体间接触面光滑.在小物块沿斜面体下滑的过程中,斜面体对小物块的作用力( )
如图所示,斜面体固定在水平面上,小物块A与斜面体间接触面光滑.在小物块沿斜面体下滑的过程中,斜面体对小物块的作用力( )