��Ŀ����
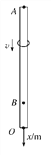
����Ŀ����ͼ��ʾ����ֱƽ���ڹ̶���һ�뾶R��1m��![]() �⻬Բ���AB��һ���Ϊ45���Ҹ�ΪH��5m��б��CD������ͨ��һˮƽ�⻬ƽ̨BC������B��ΪԲ�����͵���ƽ̨���е㡣�ֽ�����Ϊm��һС���Բ���A�����Ϸ�h����h��С�ɵ����ɾ�ֹ�ͷţ���֪�������ٶ�g��10m/s2����С���ڵ�Aʱ��Բ�����ѹ���ܱ�����͵�Bʱ��Բ�����ѹ��С3mg��
�⻬Բ���AB��һ���Ϊ45���Ҹ�ΪH��5m��б��CD������ͨ��һˮƽ�⻬ƽ̨BC������B��ΪԲ�����͵���ƽ̨���е㡣�ֽ�����Ϊm��һС���Բ���A�����Ϸ�h����h��С�ɵ����ɾ�ֹ�ͷţ���֪�������ٶ�g��10m/s2����С���ڵ�Aʱ��Բ�����ѹ���ܱ�����͵�Bʱ��Բ�����ѹ��С3mg��

��1����h��0����С����B����ٶȴ�С��
��2����h��0.8m����С����㵽C��ľ��룻��������ø�ʽ��ʾ��
��3������б���е���ֱ��һ���壬ʹ������hΪ���С����Խ�������壬��������ˮƽ�����ϣ������С����![]() Ϊ����?
����?
���𰸡���1��![]() ��2��
��2��![]() ��3��1.25m
��3��1.25m
����������1�����ͷ�С����A������ٶ���λ�ƹ�ϵ����![]()
��A�㣬����ţ�ٵڶ����ɣ�![]()
��B�㣬����ţ�ٵڶ�������![]()
����������![]()
��![]()
��![]() ����С����B����ٶ���
����С����B����ٶ���![]() ��
��
��2��С���B��C������ֱ���˶�����C�㻬������ƽ���˶�����ǡ������D����
ˮƽ������![]()
��ֱ������![]()
����Ϊб�����Ϊ![]() ����
����![]()
���![]() ����Ӧ�ĸ߶�
����Ӧ�ĸ߶�![]()
��![]() ��С������ˮƽ�����ϣ���С����B����ٶ���
��С������ˮƽ�����ϣ���С����B����ٶ���![]()
С����ƽ���˶���ֱ������![]() ������
������![]()
��ˮƽ������![]()
��С����ص��C��ľ�����![]() ��
��
��3����Ҫ������hΪ���С���Ǵ����ϣ���������ˮƽ�����ϣ��ٽ������С����ŵ�������D�㣬��ǰ�������֪����ʱ��B����ٽ��ٶ���![]()
���C����������ߵ������ˮƽ������![]()
��ֱ������![]()
����![]()
�����![]() ��
��

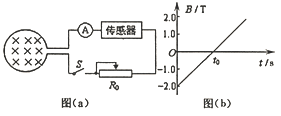
����Ŀ�����õ������͵�ѹ���ⶨһ�ڸɵ�صĵ綯�ƺ��ڵ��裮Ҫ������Сʵ����
��1��Ӧ��ѡ���ʵ���·��ͼ1�е� ��ѡ��������������������

��2�����е����������غ͵������ɣ��Լ��������ģ�
A����ѹ����0��15V��
B����ѹ����0��3V��
C��������������0��50����
D��������������0��500������
ʵ���е�ѹ��Ӧѡ�� ������������Ӧѡ�� ����ѡ����Ӧ����ǰ����ĸ��
��3��ijλͬѧ��¼��6�����������ʾ������5�����ݵĶ�Ӧ���Ѿ�����ͼ2������ֽ�ϣ���������һ�����ݵĶ�Ӧ�㣬������U��Iͼ�ߣ�
��� | 1 | 2 | 3 | 4 | 5 | 6 |
��ѹU��V�� | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
������A�� | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
��4�����ݣ�3��������ͼ�߿ɵó��ɵ�صĵ綯��E= v���ڵ���r= ��
��5��ʵ���У����Ż�����������Ƭ���ƶ�����ѹ����ʾ��U�Լ��ɵ�ص��������P���ᷢ���仯��ͼ3�ĸ�ʾ��ͼ����ȷ��ӳP��U��ϵ���� ��