题目内容
【题目】在水平地面上竖直固定一根内壁光滑的圆管，管的半径R=3.6m（管的内径大小可以忽略），管的出口A在圆心的正上方，入口B与圆心的连线与数字方向成60°角，如图所示，现有一只质量m=1kg的小球（可视为质点）从某点P以一定的初速度水平抛出，恰好从管口B处沿切线方向飞入，小球到达A时恰好与管壁无作用力，取
，求：
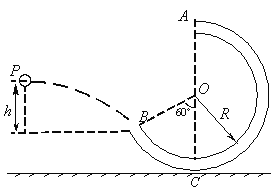
（1）小球到达圆管最高点A时的速度大小；
（2）小球在刚进入圆管B点时的速度大小；
（3）小球抛出点P到管口B的水平距离x和竖直距离h。
【答案】（1）
（2）
（3）
【解析】（1）小球在最高时对管壁无作用力，重力提供向心力，由向心力公式得： 
，可得小球到达圆管最高点时的速度为： 
。
（2）设B点的速度为
，到最高点A，由机械能守恒定律可知： 
，则整理可以得到： 
。
（3）由平抛运动规律可知，小球做平抛运动过程的初速度为： 
在B点时的竖直速度为： 
由
可知： 
由
可知，小球的抛出点到管口B的水平距离为： 
由
可得： 
。
练习册系列答案
智慧小复习系列答案
相关题目
