题目内容
7.如图甲所示,光滑且足够长的平行金属导轨MN、PQ固定在同一竖直面上,两导轨间距d=1m,电灯L的电阻R=4Ω,导轨上放一质量m=1kg、电阻r=1Ω的金属杆,长度与金属导轨等宽,与导轨接触良好,导轨的电阻不计,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场的方向垂直导轨平面向里.现用一拉力F沿竖直方向拉杆,使金属杆由静止开始向上运动,经3s上升了4m后开始做匀速运动.图乙所示为流过电灯L的电流平方随时间变化的I2-t图线,取g=10m/s2.求:(1)3s末金属杆的动能;
(2)3s末安培力的功率;
(3)4s内拉力F做的功.
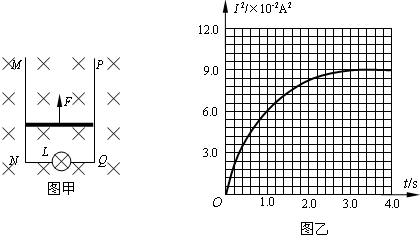
分析 (1)根据图象可知3s末的电流大小,根据结合闭合电路欧姆定律以及E=BLv,求出金属杆的速度v,从而求出金属杆的动能.
(2)3s后金属杆做匀速运动,电流不变,克服安培力做功的功率等于整个回路的发热功率.
(3)求出4s内金属杆上升的位移,根据能量守恒W=Q+mgH+EK求出4s内拉力F做的功.
解答 解:(1)由I2-t图可得:t=3s时电流I=0.3A;
感应电动势为:E=Blv=I(R+r)=1.5V
代入数据解得:v=3m/s,
金属杆的动能:EK=$\frac{1}{2}$mv2=$\frac{1}{2}$×1×32=4.5J;
(2)安培力为:F=BIL=$\frac{{B}^{2}{L}^{2}v}{R+r}$,
安培力的功率为:P=Fv=$\frac{{B}^{2}{L}^{2}{v}^{2}}{R+r}$=0.45W;
(3)由能量守恒定律得:W=mgh+I2(R+r)t+$\frac{1}{2}$mv2,
代入数据解得:W=75.94J;
答:(1)3s末金属杆的动能为4.5J;
(2)3s末安培力的功率为0.45W;
(3)4s内拉力F做的功为75.94J.
点评 解决本题的关键掌握E=BLv和熟练运用闭合电路欧姆定律,以及知道克服安培力做功的功率等于整个回路的发热功率.

练习册系列答案
相关题目
17. 如图所示的电路,L是小灯泡,C是极板水平放置的平行板电容 器.有一带电油滴悬浮在两极板间静止不动.若滑动变阻器的滑片向下滑动,则( )
如图所示的电路,L是小灯泡,C是极板水平放置的平行板电容 器.有一带电油滴悬浮在两极板间静止不动.若滑动变阻器的滑片向下滑动,则( )
 如图所示的电路,L是小灯泡,C是极板水平放置的平行板电容 器.有一带电油滴悬浮在两极板间静止不动.若滑动变阻器的滑片向下滑动,则( )
如图所示的电路,L是小灯泡,C是极板水平放置的平行板电容 器.有一带电油滴悬浮在两极板间静止不动.若滑动变阻器的滑片向下滑动,则( )| A. | L变亮 | B. | L亮度不变 | C. | 油滴向上运动 | D. | 油滴向下运动 |
15.绕地球做匀速圆周运动的人造地球卫星,如果其轨道半径增大到原来的2倍,则卫星的线速度将( )
| A. | 增大到原来的2倍 | B. | 增大到原来的$\sqrt{2}$倍 | C. | 减小到原来的$\frac{1}{2}$ | D. | 减小到原来的$\frac{\sqrt{2}}{2}$ |
2.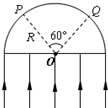 平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现只有P、Q之间所对圆心角为60°的球面上有光射出,若仅将a平行光换成b平行光,测得有光射出的范围增大,设玻璃球对a和b两种色光折射率分别为na和nb,光子能量分别为Ea和Eb.则( )
平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现只有P、Q之间所对圆心角为60°的球面上有光射出,若仅将a平行光换成b平行光,测得有光射出的范围增大,设玻璃球对a和b两种色光折射率分别为na和nb,光子能量分别为Ea和Eb.则( )
 平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现只有P、Q之间所对圆心角为60°的球面上有光射出,若仅将a平行光换成b平行光,测得有光射出的范围增大,设玻璃球对a和b两种色光折射率分别为na和nb,光子能量分别为Ea和Eb.则( )
平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现只有P、Q之间所对圆心角为60°的球面上有光射出,若仅将a平行光换成b平行光,测得有光射出的范围增大,设玻璃球对a和b两种色光折射率分别为na和nb,光子能量分别为Ea和Eb.则( )| A. | na>nb、Ea>Eb | B. | na>nb、Ea<Eb | C. | na<nb、Ea>Eb | D. | na<nb、Ea<Eb |
19.两列频率相同的波发生干涉时,若两列波的波谷在某质点P位置相遇,则( )
| A. | 质点P的振幅随时间周期性变化 | |
| B. | 质点P的振动始终减弱,P点振幅最小 | |
| C. | 质点P的振动始终加强,P点振幅最大 | |
| D. | 质点P的振动始终减弱,P点位移始终最小 |
16.一质点沿x轴运动,其位置x随时间t变化的规律为:x=10+10t-5t2(m),t的单位为s,下列关于该质点运动的说法正确的是( )
| A. | 该质点的加速度大小为5m/s2 | |
| B. | 物体回到x=0处时其速度大小为5m/s | |
| C. | t=2s时刻该质点速度大小为10m/s | |
| D. | 0~3s内该质点的平均速度大小为10m/s |
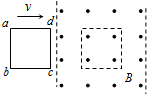 如图所示,单匝线圈abcd在外力作用下以速度v向右匀速进入匀强磁场,第二次以速度2v匀速进入同一匀强磁场.第一次与第二次线圈中感应电流之比为1:2,回路中产生的焦耳热之比为1:2.
如图所示,单匝线圈abcd在外力作用下以速度v向右匀速进入匀强磁场,第二次以速度2v匀速进入同一匀强磁场.第一次与第二次线圈中感应电流之比为1:2,回路中产生的焦耳热之比为1:2.