题目内容
(2009?重庆)据报道,“嫦娥一号”和“嫦娥二号”绕月飞行器的圆形轨道距月球表面分别约为200Km和100Km,运动速率分别为v1和v2,那么v1和v2的比值为(月球半径取1700Km)( )
分析:研究卫星绕月球做匀速圆周运动,根据万有引力提供向心力,列出等式表示出速度.
根据题目中已知量的关系求出v1和v2的比值.
根据题目中已知量的关系求出v1和v2的比值.
解答:解:“嫦娥一号”和“嫦娥二号”绕月作圆周运动,由万有引力提供向心力有
=
可得V=
(M为月球质量,R为轨道半径),
它们的轨道半径分R1=1900Km、R2=1800Km,
则v1:v2=
=
.
故选C.
| GMm |
| R2 |
| mV2 |
| R |
可得V=
|
它们的轨道半径分R1=1900Km、R2=1800Km,
则v1:v2=
|
|
故选C.
点评:本题考查了万有引力在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.
求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再进行之比.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.
求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再进行之比.

练习册系列答案
相关题目
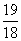 B.
B.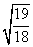 C.
C.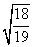 D.
D.