题目内容
一列货车以8m/s的速度在平直铁路上运行,由于调度失误,在后面600m处有一列快车以20m/s的速度向它靠近.快车司机发觉后立即制动,若两车恰好不相撞,(货车速度保持不变)求:
(1)快车从制动至两车恰好不相撞所用时间t;
(2)快车制动过程中的加速度a的大小;
(3)从制动至两车恰好不相撞快车的位移的大小.
解:(1)因为只要快车速度大于货车速度,两车的距离就在逐渐减小,直到两车相撞;当两车速度相等时两车没有相撞,则以后就不会相撞,所以在客车匀减速运动中当速度相等时,正好相遇,则有:
货车的位移为:x1=8t
快车的位移为: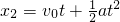
at=8
x1+600=x2
联立方程解得:t=100s
(2)由v=v0+at
得:a=0.12m/s2
(3)快车的位移为: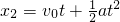 =1400m
=1400m
答:(1)快车从制动至两车恰好不相撞所用时间为100s;
(2)快车制动过程中的加速度a的大小为0.12m/s2;
(3)从制动至两车恰好不相撞快车的位移的大小为1400m.
分析:快车做匀减速直线运动运动,货车做匀速直线运动,两车能否相撞看客车速度减到和货车相等时,快车的位移与货车的位移与两者距离600m的关系,大于或等于600m则相撞,小于则不相撞.客车的位移据匀减速直线运动规律求解.
点评:注意判断两车是否相撞的条件,即当客车速度减为货车速度时判断是否相撞,而不是判断客车速度减为0时刻相撞.许多同学会默认比较客车速度减为0的位移和货车位移之间的关系,这是错误的判断.
货车的位移为:x1=8t
快车的位移为:
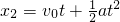
at=8
x1+600=x2
联立方程解得:t=100s
(2)由v=v0+at
得:a=0.12m/s2
(3)快车的位移为:
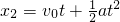 =1400m
=1400m答:(1)快车从制动至两车恰好不相撞所用时间为100s;
(2)快车制动过程中的加速度a的大小为0.12m/s2;
(3)从制动至两车恰好不相撞快车的位移的大小为1400m.
分析:快车做匀减速直线运动运动,货车做匀速直线运动,两车能否相撞看客车速度减到和货车相等时,快车的位移与货车的位移与两者距离600m的关系,大于或等于600m则相撞,小于则不相撞.客车的位移据匀减速直线运动规律求解.
点评:注意判断两车是否相撞的条件,即当客车速度减为货车速度时判断是否相撞,而不是判断客车速度减为0时刻相撞.许多同学会默认比较客车速度减为0的位移和货车位移之间的关系,这是错误的判断.

练习册系列答案
相关题目