Question

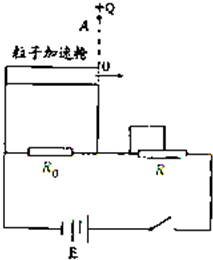
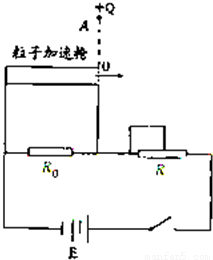
如图所示，由电源、定值电阻R₀和滑动变阻器R构成一闭合电路，一粒子加速枪并接在R₀两端，在加速枪口O正上方r处的A点真空区域有一固定的点电荷，带电量为+Q．现有质量和带电量均不同的两种带负电静止粒子，从加速枪的左端加速后从O点进入+Q场区域，粒子射入枪口时速度方向垂直于AO连线．
（1）试证明若加速电压U满足一定条件，两种粒子在+Q场区域都能做匀速圆周运动．（不计粒子的重力）
（2）当滑动变阻器滑动头在某位置时，射出的带电粒子恰好做匀速圆周运动，若将P向左移动一小段距离后，该种粒子从加速枪中射出后的运轨迹变成什么形状？它的周期比圆周运动时长还是短？（只写明最后结论）

Answer 1

分析：（1）带电粒子在电场中被加速，由动能定理可求出加速获得的速度；当进入点电荷电场中做匀速圆周运动，由电场力提供向心力，则由牛顿第二定律列出表达式，从而求出加速电压满足的条件，因此得以证明．
（2）若将P向左移动一小段距离后，加速枪的电压减小，粒子加速获得的速度减小，粒子将做椭圆运动，周期变短．

解答：解：（1）设带电粒子电量为q，质量为m，射出速度为v．
由动能定理：qU=

1

2

mv2
在库仑力作用下做匀速圆周运动，由向心力公式：K

qQ

r2

=m

v2

r

解得U=

KQ

2r

由U满足条件看出：U与带电粒子q、m均无关．故两种粒子在+Q场区域都能做匀速圆周运动．
（2）若将P向左移动一小段距离后，加速枪的电压减小，粒子加速获得的速度减小，粒子将做椭圆运动，周期变短．

点评：此题考查动能定理、库仑定律、牛顿第二定律等规律，并涉及到向心力公式．特别关注电场力提供向心力，此处的电场力不做功，只改变带电粒子的速度方向．