题目内容
12.光子的动量p与波长λ的关系为p=$\frac{h}{λ}$,静止的原子核放出一个波长为λ的光子,已知普朗克常量为h,光在真空中传播的速度为c,求:(1)质量为M的反冲核的速度为多少?
(2)反冲核运动时物质波的波长是多少?
分析 (1)原子核放出光子的过程中,动量守恒,根据动量守恒定律即可求解;
(2)根据p=$\frac{h}{λ}$求出反冲核运动时物质波的波长.
解答 解:(1)原子核放出光子的过程中,动量守恒,设光子的速度方向为正,
根据动量守恒定律得:
$\frac{h}{λ}-Mv=0$
解得:v=$\frac{h}{λM}$
(2)反冲核运动时物质波的波长$λ=\frac{h}{P′}=\frac{h}{Mv}=λ$
答:(1)质量为M的反冲核的速度为$\frac{h}{λM}$;
(2)反冲核运动时物质波的波长是λ.
点评 本题主要考查了动量守恒定律的直接应用,知道静止的原子核放出光子的过程中,动量是守恒的,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.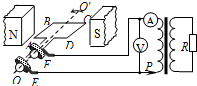 如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )
如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )
 如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )
如图所示,面积为0.02m2、内阻不计的100匝矩形线圈ABCD,绕垂直于磁场的轴OO′匀速转动,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\frac{\sqrt{2}}{2}$T.矩形线圈通过滑环与理想变压器相连,触头P可移动,副线圈所接电阻R=50Ω,电表均为理想交流电表.当线圈平面与磁场方向平行时开始计时.下列说法正确的是( )| A. | 线圈中感应电动势的表达式为e=10$\sqrt{2}$cos(100t)V | |
| B. | P上移时,电流表示数减小 | |
| C. | t=0时,电压表示数为10$\sqrt{2}$V | |
| D. | 当原、副线圈匝数比为2:1时,电阻上消耗的功率为50W |
3.有关开普勒关于行星运动的描述,下列说法中不正确的是( )
| A. | 所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上 | |
| B. | 所有行星均是以同样的速度绕太阳运动 | |
| C. | 所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等 | |
| D. | 不同的行星绕太阳运动的椭圆轨道是不同的 |
17.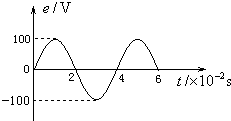 某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
 某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
某交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间的关系如图所示.如果此线圈和一个R=100Ω 的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )| A. | 交变电流的周期为0.04s | B. | 电阻R两端的有效电压是100V | ||
| C. | 交变电流的有效值为1A | D. | 交变电流的最大值为1A |

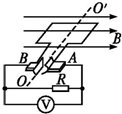 如图所示,匀强磁场的磁感应强度B=$\sqrt{2}$T,边长L=10cm的正方形线圈共100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2rad/s,外电路中的电阻R=4Ω,求:
如图所示,匀强磁场的磁感应强度B=$\sqrt{2}$T,边长L=10cm的正方形线圈共100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO'匀速转动,角速度ω=2rad/s,外电路中的电阻R=4Ω,求: