题目内容
一个物体质量为2kg,受到一个斜向上与水平面成370角,大小为20N的拉力F作用下从静止出发,水平前行,物块与水平地面的摩擦因素为μ=0.2,当物体滑行10米距离时,撤去拉力F,(g=10m/s2,sin37°=0.6,cos37°=0.8),求:
(1)拉力F作用的过程,合外力对物体做的功W合
(2)拉力F做功的平均功率P平均
(3)撤去拉力后,物体还可以滑行的距离S.
(1)拉力F作用的过程,合外力对物体做的功W合
(2)拉力F做功的平均功率P平均
(3)撤去拉力后,物体还可以滑行的距离S.
分析:(1)对物体受力分析,运用正交分解求出合力的大小,从而求出合力做功的大小.
(2)根据牛顿第二定律求出加速度,从而根据位移时间公式求出时间的大小,通过F做功的大小,求出平均功率的大小.
(3)撤去F后,根据牛顿第二定律求出加速度,结合匀加速直线运动的末速度,通过速度位移公式求出还能滑行的距离.
(2)根据牛顿第二定律求出加速度,从而根据位移时间公式求出时间的大小,通过F做功的大小,求出平均功率的大小.
(3)撤去F后,根据牛顿第二定律求出加速度,结合匀加速直线运动的末速度,通过速度位移公式求出还能滑行的距离.
解答:解:(1)物体所受的合力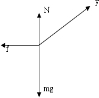 F合=Fcos37°-μ(mg-Fsin37°)=20×0.8-0.2×(20-20×0.6)N=14.4N.
F合=Fcos37°-μ(mg-Fsin37°)=20×0.8-0.2×(20-20×0.6)N=14.4N.
则合力做功W合=F合s=14.4×10J=144J.
(2)拉力做功的大小W=Fscos37°=20×10×0.8J=160J.
根据牛顿第二定律得,物体的加速度a=
=
m/s2=7.2m/s2.
根据s=
at2得,t=
=
s≈2.8s.
则拉力做功的平均功率P=
=
≈57W.
(3)根据速度时间公式得,v=at
匀减速直线运动的加速度a′=μg=2m/s2.
则继续滑行的距离s=
=
=
=
m=36m.
答:(1)合外力对物体做的功为144J
(2)拉力F做功的平均功率为57W.
(3)撤去拉力后,物体还可以滑行的距为36m.
 F合=Fcos37°-μ(mg-Fsin37°)=20×0.8-0.2×(20-20×0.6)N=14.4N.
F合=Fcos37°-μ(mg-Fsin37°)=20×0.8-0.2×(20-20×0.6)N=14.4N.则合力做功W合=F合s=14.4×10J=144J.
(2)拉力做功的大小W=Fscos37°=20×10×0.8J=160J.
根据牛顿第二定律得,物体的加速度a=
| F合 |
| m |
| 14.4 |
| 2 |
根据s=
| 1 |
| 2 |
|
|
则拉力做功的平均功率P=
| W |
| t |
| 160 |
| 2.8 |
(3)根据速度时间公式得,v=at
匀减速直线运动的加速度a′=μg=2m/s2.
则继续滑行的距离s=
| v2 |
| 2a′ |
| a2t2 |
| 2a′ |
| 2as |
| 2a′ |
| 2×7.2×10 |
| 2×2 |
答:(1)合外力对物体做的功为144J
(2)拉力F做功的平均功率为57W.
(3)撤去拉力后,物体还可以滑行的距为36m.
点评:本题考查了牛顿第二定律、运动学公式的综合,对于第三问,也可以通过动能定理进行求解.

练习册系列答案
相关题目
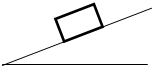 一个物体质量为2kg,从倾角为37°的斜面底端往上滑动,已知物体与斜面的动摩擦因数为0.5,则物体的加速度为多大?(g=10m/s2,要求画出正确的受力分析图,此图2分)
一个物体质量为2kg,从倾角为37°的斜面底端往上滑动,已知物体与斜面的动摩擦因数为0.5,则物体的加速度为多大?(g=10m/s2,要求画出正确的受力分析图,此图2分)
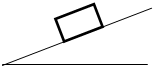 一个物体质量为2kg,从倾角为37°的斜面底端往上滑动,已知物体与斜面的动摩擦因数为0.5,则物体的加速度为多大?(g=10m/s2,要求画出正确的受力分析图,此图2分)
一个物体质量为2kg,从倾角为37°的斜面底端往上滑动,已知物体与斜面的动摩擦因数为0.5,则物体的加速度为多大?(g=10m/s2,要求画出正确的受力分析图,此图2分)