题目内容
4. 如图所示,在真空室中平面直角坐标系的y轴竖直向上,x轴上的P点与Q点关于坐标原点O对称,PQ间的距离d=30cm.坐标系所在空间存在一匀强电场,场强的大小E=1.0N/C.一带电油滴在xOy平面内,从P点与x轴成30°的夹角射出,该油滴将做匀速直线运动,已知油滴的速度v=2.0m/s射出,所带电荷量q=1.0×10-7C,重力加速度为g=10m/s2.
如图所示,在真空室中平面直角坐标系的y轴竖直向上,x轴上的P点与Q点关于坐标原点O对称,PQ间的距离d=30cm.坐标系所在空间存在一匀强电场,场强的大小E=1.0N/C.一带电油滴在xOy平面内,从P点与x轴成30°的夹角射出,该油滴将做匀速直线运动,已知油滴的速度v=2.0m/s射出,所带电荷量q=1.0×10-7C,重力加速度为g=10m/s2.(1)求油滴的质量m.
(2)若在空间叠加一个垂直于xOy平面的圆形有界匀强磁场,使油滴通过Q点,且其运动轨迹关于y轴对称.已知磁场的磁感应强度大小为B=2.0T,求:
a.油滴在磁场中运动的时间t;
b.圆形磁场区域的最小面积S.
分析 (1)对带电油滴进行受力分析,根据牛顿运动定律即可求解;
(2)带电油滴进入匀强磁场,其轨迹如图所示,根据向心力公式、求出半径,进而求出周期,根据几何关系求出圆心角,继而求出粒子在磁场中运动的时间,由题意可知,油滴在P到M和N到Q的过程中做匀速直线运动,且运动时间相等.根据几何关系和速度公式求解粒子在这两段运动过程中的时间,三段运动时间之和即为总时间,连接MN,当MN为圆形磁场的直径时,圆形磁场面积最小,根据几何关系求出半径,S=πr2求解面积
解答  解:(1)对带电油滴进行受力分析,根据牛顿运动定律有:
解:(1)对带电油滴进行受力分析,根据牛顿运动定律有:
qE-mg=0
所以$m=\frac{qE}{g}=1.0×1{0}^{-8}kg$
(2)带电油滴进入匀强磁场,其轨迹如图所示,设其做匀速圆周运动设圆周运动的半径为R、运动周期为T、油滴在磁场中运动的时间为t,根据牛顿第二定律:
所以$Bqv=\frac{{mv}^{2}}{R}$
解得:R=$\frac{mv}{Bq}=0.10m$
所以$T=\frac{2πr}{v}=0.1πs$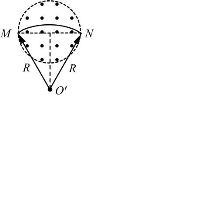 设带电油滴从M点进入磁场,从N点射出磁场,由于油滴的运动轨迹关于y轴对称,如图所示,根据几何关系可知∠MO'N=60°,所以,带电油滴在磁场中运动的时间
设带电油滴从M点进入磁场,从N点射出磁场,由于油滴的运动轨迹关于y轴对称,如图所示,根据几何关系可知∠MO'N=60°,所以,带电油滴在磁场中运动的时间
${t}_{2}=\frac{T}{6}=\frac{0.1π}{6}$s
由题意可知,油滴在P到M和N到Q的过程中做匀速直线运动,且运动时间相等.根据几何关系可知,
$PM=NQ=\frac{\frac{d}{2}-Rsin30°}{cos30°}=\frac{0.2}{3}\sqrt{3}m$
所以油滴在P到M和N到Q过程中的运动时间为:${t}_{1}={t}_{3}=\frac{PM}{v}=\frac{0.1}{3}\sqrt{3}$s
则油滴从P到Q运动的时间为:$t={t}_{1}+{t}_{2}+{t}_{3}=(\frac{0.2}{3}\sqrt{3}+\frac{0.1π}{6})s=0.17s$
(3)连接MN,当MN为圆形磁场的直径时,圆形磁场面积最小,如图所示.根据几何关系圆形磁场的半径
r=Rsin30°=0.05m
其面积为:S=πr2=0.0025πm2=7.9×10-3m2.
答::(1)求油滴的质量m为1.0×10-8kg.
(2)a.油滴在磁场中运动的时间为0.17s;
b.圆形磁场区域的最小面积S为7.9×10-3m2.
点评 本题关键是先确定油滴的运动情况,并画出运动轨迹,然后逐段逐段分析,匀速圆周运动阶段洛伦兹力提供向心力,并结合几何知识求解,难度适中.

| A. | 在不同的惯性参考系中,真空中的光速都是相同的 | |
| B. | 时间的测量结果与物体相对观察者的运动状态无关 | |
| C. | 高速运动的物体,沿运动方向的长度会变长 | |
| D. | 对于确定的物体,无论运动速度由多大,物体的质量都不会改变 |
 某小水力发电站发电机输出的电压,先通过电站附近的升压变压器升压后,再用高压输电线路把电能输送到远处的降压变压器.降压后,再用线路接到各用户.图示为输电原理图,设发电机输出电压稳定且两变压器均为理想变压器,当用户用电量增大时( )
某小水力发电站发电机输出的电压,先通过电站附近的升压变压器升压后,再用高压输电线路把电能输送到远处的降压变压器.降压后,再用线路接到各用户.图示为输电原理图,设发电机输出电压稳定且两变压器均为理想变压器,当用户用电量增大时( )| A. | 压输电线路的电压损失变大 | |
| B. | 升压变压器的副线圈两端的电流变大 | |
| C. | 降压变压器的副线圈中的电流变大 | |
| D. | 用户获得的电压变大 |
 如图所示,在一根张紧的绳上挂着四个单摆,其中甲、丙两单摆的摆长相等.现给甲摆一个初始能量,使其开始摆动.摆动稳定后,关于乙、丙、丁三个单摆,下列说法正确的是( )
如图所示,在一根张紧的绳上挂着四个单摆,其中甲、丙两单摆的摆长相等.现给甲摆一个初始能量,使其开始摆动.摆动稳定后,关于乙、丙、丁三个单摆,下列说法正确的是( )| A. | 乙摆摆动的周期与甲摆摆动的周期相同 | |
| B. | 丁摆摆动的周期与丙摆摆动的周期相同 | |
| C. | 丁摆频率最大 | |
| D. | 乙摆振幅最大 | |
| E. | 丙摆振幅最大 |

| A. | 0~t1时间内物块的加速度不为零 | |
| B. | t2时刻物块A的加速度最大 | |
| C. | t3时刻物块A的速度最大 | |
| D. | 0~t3时间内F对物块A先做正功后做负功 |

| A. | a | B. | b | C. | c | D. | d |
| A. | 质量不同的同步卫星,角速度不同 | |
| B. | 质量不同的同步卫星,线速度大小不同 | |
| C. | 质量不同的同步卫星,其轨道高度不同 | |
| D. | 所有地球同步卫星的加速度大小都相同 |
 交流发电机转子有n匝矩形线圈,每匝线圈所围面积为S,匀强磁场的磁感应强度为B,匀速转动的角速度为ω,线圈内电阻为r,外电路电阻为R.当线圈由图中实线位置匀速转动90°到达虚线位置过程中,问:
交流发电机转子有n匝矩形线圈,每匝线圈所围面积为S,匀强磁场的磁感应强度为B,匀速转动的角速度为ω,线圈内电阻为r,外电路电阻为R.当线圈由图中实线位置匀速转动90°到达虚线位置过程中,问: 北斗卫星导航系统是中国自行研制开发的区域性有源三维卫星定位与通信系统(CNSS),其空间端包括5颗静止轨道卫星和30颗非静止轨道卫星,如图甲所示,为简便起见,认为其中一颗卫星轨道平面与地球赤道平面重合,绕地心做匀速圆周运动(如图乙所示).已知地球表面重力加速度为g,地球的半径R,该卫星绕地球匀速圆周运动的周期为T,求该卫星绕地球作匀速圆周运动的轨道半径r.
北斗卫星导航系统是中国自行研制开发的区域性有源三维卫星定位与通信系统(CNSS),其空间端包括5颗静止轨道卫星和30颗非静止轨道卫星,如图甲所示,为简便起见,认为其中一颗卫星轨道平面与地球赤道平面重合,绕地心做匀速圆周运动(如图乙所示).已知地球表面重力加速度为g,地球的半径R,该卫星绕地球匀速圆周运动的周期为T,求该卫星绕地球作匀速圆周运动的轨道半径r.