��Ŀ����
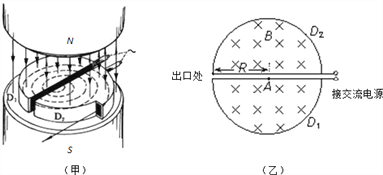
����Ŀ��1932����������ѧ������˹�����˻�������������������ô��������ڴų��е��˶��ص㣬��������ӵļ������⣮���ڻ������������㷺Ӧ���ڿ�ѧ�о���ҽѧ�豸�У�ij�ͺŵĻ����������Ĺ���ԭ����ͼ���ף���ʾ��ͼ���ң�Ϊ����ͼ�������������ĺ��IJ���Ϊ����D�κУ��ֱ�ΪD1��D2��D�κ�װ��������������װ�÷��ھ�ĵ��������֮���ǿ��ų��У��ų�������Ϊ����ǿ�ų�������D�κе��洹ֱ�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ�D�κеİ뾶ΪR���ų��ĴŸ�Ӧǿ��ΪB�������Ӵ�����ԴA��������ٵ糡�ij��ٶȲ��ƣ���������Ϊm�������Ϊ+q������������һ��Ƶ�ʵĸ�Ƶ�����Դ�����ٵ�ѹΪU�����ٹ����в����������ЧӦ���������ã�
��1�������ӵ�1�ξ������챻���ٺ����D2��ʱ���ٶȴ�Сv1��
��2�������ӵ�1�ξ������챻���ٺ����D2�к��˶��Ĺ���뾶r1��
��3�������ӴӾ�ֹ��ʼ���ٵ����ڴ������ʱ��t��
���𰸡���1�����ӵ�1�ξ������챻���ٺ����D2��ʱ���ٶȴ�Сv1Ϊ![]() ��
��
��2�����ӵ�1�ξ������챻���ٺ����D2�к��˶��Ĺ���뾶r1Ϊ![]()
![]() ��
��
��3�����ӴӾ�ֹ��ʼ���ٵ����ڴ������ʱ��tΪ![]() ��
��
�������������������1�����ݶ��ܶ���������ӵ�1�ξ������챻���ٺ����D2��ʱ���ٶȴ�С��
��2���������ӵ��ٶȣ�ͨ�����������ṩ��������������ڴų����˶��Ĺ���뾶��
��3������D�κеİ뾶�ó����ӵ�����ٶȣ�ͨ�����ܶ���������ٵĴ������Ӷ����������ڴų����˶�������������ӴӾ�ֹ��ʼ���ٵ����ڴ������ʱ��t��
�⣺��1�����ݶ��ܶ����ã�qU=![]() mv12��
mv12��
��ã�v1=![]() ��
��
��2������ţ�ٵڶ����ɵã�qv1B=m![]() ��
��
��ã�r1=![]()
![]() ��
��
��3�������ӴӾ�ֹ��ʼ���ٵ����ڴ���������nȦ�������ڳ��ڴ����ٶ�Ϊv��
���ݶ��ܶ����ã�2nqU=![]() mv2��
mv2��
����ţ�ٵڶ����ɵã�qvB=m![]() ��
��
������Բ���˶������ڣ�T=![]() =
=![]() ��
��
���ӵ��˶�ʱ�䣺t=nT��
��ã�t=![]() ��
��
�𣺣�1�����ӵ�1�ξ������챻���ٺ����D2��ʱ���ٶȴ�Сv1Ϊ![]() ��
��
��2�����ӵ�1�ξ������챻���ٺ����D2�к��˶��Ĺ���뾶r1Ϊ![]()
![]() ��
��
��3�����ӴӾ�ֹ��ʼ���ٵ����ڴ������ʱ��tΪ![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��������λͬѧ���ô�������ʱ����ֽ������¼С�����˶�������ʱ�����õ�Դ��Ƶ��Ϊ50Hz��
��1���йز����Ͳ�����˵������ȷ����_____
A�����ͷ�С�����ٽ�ͨ��Դ����С�����ﻬ��ǰ��ʱ���ְ�ס����رյ�Դ
B����ʼ�ͷ�С��ǰ��ӦʹС����������ʱ��
C������ʱӦ��ȥֽ���ϵ��ܼ��㣬Ȼ��ѡȡ������
D������ÿ5����ӡ����һ��������
��2��ʵ���ͬѧѡ����һ����Ϊ�����ֽ�����������ݺ�ͨ������õ���С���˶������и���ʱʱ�̵��ٶ��������ʾ��
λ�ñ�� | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
ʱ��t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
�ٶ�v/ms��1 | 0.42 | 0.67 | 0.92 | 1.16 | 1.42 |
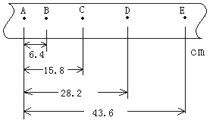
�����������ݣ�����������ķ�Χ�ڣ�С����_____�˶������ڴ˴�ʵ���ԭʼֽ��û�б��棬��ͬѧ�����С����λ��0��λ��5��λ�ƣ�������㷽�����£�x=��0.42��0.1+0.67��0.1+0.92��0.1+1.16��0.1+1.42��0.1��m����ô����ͬѧ�õ���λ��_____��ѡ������������������������С������ʵ��λ�ƣ�
��3��ijͬѧ���ô���ʱ������¼��ֽ�����о�С�����ȱ���ֱ���˶��������ʵ���л��һ��ֽ������ͼ�����������ڼ��������������δ��������֪���õ�Դ��Ƶ��Ϊ50Hz�����B��ʱС���˶����ٶȴ�СvB=_____m/s��С���˶��ļ��ٶȴ�Сa=_____m/s2��������������3λ��Ч���֣�