题目内容
【题目】如图所示，固定斜面的倾角θ=30°，物体A与斜面之间的动摩擦因数=
，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于C点.用一根不可伸长的轻绳，通过轻质光滑的定滑轮连接物体A和B，滑轮右侧绳子与斜面平行，A的质量为mA=2kg，B的质量为mB=1kg，物体A的初始位置到C点的距离为L=0.5m.现给A、B一初速度v0=3m/s，使A沿斜面向下运动，B向上运动，物体A将弹簧压缩到最短后又恰好能弹到C点.已知重力加速度g=10m/s2，不计空气阻力，整个过程中轻绳始终处于伸直状态，求：
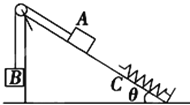
（1）物体A向下运动，刚到C点时的速度大小.
（2）弹簧的最大压缩量.
（3）弹簧的最大弹性势能.
【答案】（1）
（2）x=0.2m（3）3J
【解析】（1）在物体A向下运动，刚到C点时过程中，对A和B整体，由动能定理：
）
故
（2）设弹簧的最大压缩量为x，在物体A刚到C点至压缩弹簧又返回C点的过程中，由能量守恒： 
，得
（3）设弹簧的最大弹性势能为EP，在物体A刚到C点至压缩弹簧到最短的过程中，由功能关系： 
，故
.
练习册系列答案
相关题目
