题目内容
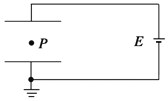
【题目】如图所示,两足够长的光滑金属导轨竖直放置,相距L=1 m,一理想电流表和一电阻R=10 Ω的电阻通过导线与两导轨相连,导轨之间存在着方向相同,高度均为h的匀强磁场Ⅰ、Ⅱ,匀强磁场与导轨平面垂直。一质量为m=1 kg、有效电阻也为R=10 Ω的导体棒,从距磁场Ⅰ下方边界一定距离处,在F=20 N的恒定外力作用下从静止开始竖直向上运动,导体棒在Ⅰ磁场中运动的过程中电流表的示数恒为1 A,导体棒离开磁场Ⅱ前的一段时间内电流表的示数恒为2 A,导体棒始终保持水平,不计导轨的电阻。(g=10 m/s2)求:
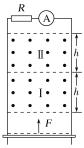
(1)Ⅰ、Ⅱ两磁场的磁感应强度分别为多大;
(2)导体棒开始运动的位置到磁场Ⅰ下端的距离。
【答案】(1) 10 T 5 T (2)0.2 m
【解析】
根据“在F=20 N的恒定外力作用下从静止开始竖直向上运动”、“导体棒在Ⅰ磁场中运动的过程中电流表的示数恒为1 A”、“导体棒离开磁场Ⅱ前的一段时间内电流表的示数恒为2 A”可知,本题考查导体棒在匀强磁场中匀速运动问题,根据平衡条件和闭合电路欧姆定律列方程求解磁感应强度大小;根据动能定理求解导体棒开始运动的位置到磁场Ⅰ下端的距离。
(1)导体棒进入Ⅰ磁场时,导体棒做匀速运动,根据平衡条件得F=mg+B1I1L
解得B1=10 T
导体棒离开Ⅱ磁场时,导体棒做匀速运动,根据平衡条件得F=mg+B2I2L
解得B2=5 T
(2)设导体棒进入Ⅰ磁场时的速度为v1,
由I1=![]() =
=![]()
解得v1=![]() =2 m/s
=2 m/s
设从导体棒开始运动的位置到磁场Ⅰ下端的距离为d,根据动能定理得(F-mg)d=![]() mv
mv
解得d=0.2 m
答案 (1) 10T,5 T (2)0.2 m

练习册系列答案
相关题目