题目内容
8. 如图所示,质量为2m的小滑块P和质量为m的小滑块Q都视作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v向Q运动并与弹簧发生碰撞,当弹簧的弹性势能最大时,P的速度大小是$\frac{2}{3}$v,此时弹簧的最大弹性势能为$\frac{1}{3}$mv2.
如图所示,质量为2m的小滑块P和质量为m的小滑块Q都视作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v向Q运动并与弹簧发生碰撞,当弹簧的弹性势能最大时,P的速度大小是$\frac{2}{3}$v,此时弹簧的最大弹性势能为$\frac{1}{3}$mv2.
分析 P、Q碰撞过程系统动量守恒、机械能守恒,当两者速度相等时弹簧的压缩量最大,应用动量守恒定律与机械能守恒定律可以求出速度与弹性势能.
解答 解:P、Q速度相等时弹簧的弹性势能最大,系统动量守恒,以向右为正方向,由动量守恒定律得:
2mv=(2m+m)v′,
解得:v′=$\frac{2}{3}$v,
由机械能守恒定律的:$\frac{1}{2}$•2mv2=$\frac{1}{2}$(2m+m)v′2+EP,
解得:EP=$\frac{1}{3}$mv2;
故答案为:$\frac{2}{3}v$;$\frac{1}{3}m{v^2}$.
点评 碰撞过程系统机械能守恒、动量守恒,应用动量守恒定律与机械能守恒定律可以解题;分析清楚物体运动过程、知道两者速度相等时弹簧的弹性势能最大是正确解题的关键.

练习册系列答案
相关题目
18.如图1所示某同学探究弹力与弹簧伸长量的关系
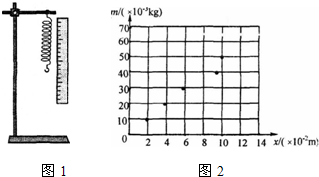
①将弹簧悬挂在铁架台上,将最小刻度为毫米的刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在竖直方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧稳定时,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:
表中有一个数值记录不规范,代表符号为L3
③该同学在坐标纸上取砝码的质量为纵轴,弹簧长度与Lx的差值为横轴,如图是他根据表中数据已经描好的前5个点,请描出第6个点并完成该图象
④由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g(结果保留两位有效数字,重力加速度取9.8m/s2)

①将弹簧悬挂在铁架台上,将最小刻度为毫米的刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在竖直方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧稳定时,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:
| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 37.15 | 37.45 | 39.30 |
③该同学在坐标纸上取砝码的质量为纵轴,弹簧长度与Lx的差值为横轴,如图是他根据表中数据已经描好的前5个点,请描出第6个点并完成该图象
④由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g(结果保留两位有效数字,重力加速度取9.8m/s2)
19. 如图所示,有相同的两个物块A、B叠放在地面上,各接触面之间的动摩擦因数均为μ.今在B物块上施加一个大小为F、方向向右的水平拉力,两个物块均保持静止状态,则( )
如图所示,有相同的两个物块A、B叠放在地面上,各接触面之间的动摩擦因数均为μ.今在B物块上施加一个大小为F、方向向右的水平拉力,两个物块均保持静止状态,则( )
 如图所示,有相同的两个物块A、B叠放在地面上,各接触面之间的动摩擦因数均为μ.今在B物块上施加一个大小为F、方向向右的水平拉力,两个物块均保持静止状态,则( )
如图所示,有相同的两个物块A、B叠放在地面上,各接触面之间的动摩擦因数均为μ.今在B物块上施加一个大小为F、方向向右的水平拉力,两个物块均保持静止状态,则( )| A. | 物块A受到B的摩擦力,方向向右 | B. | 物块B不受A的摩擦力作用 | ||
| C. | 地面C对物块B的摩擦力方向向左 | D. | 地面C不受摩擦力的作用 |
3.由下列哪些现象可以说明光是横波( )
| A. | 光的偏振现象 | B. | 光的色散现象 | ||
| C. | 光的全反射现象 | D. | 光的干涉和衍射现象 |
13. 如图,一质量为m的正方体物块置于风洞内的水平面上,其一面与风速垂直,当风速为v0时刚好能推动该物块.已知风对物块的推力F正比于Sv2,其中v为风速、S为物块迎风面积.当风速变为2v0时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为( )
如图,一质量为m的正方体物块置于风洞内的水平面上,其一面与风速垂直,当风速为v0时刚好能推动该物块.已知风对物块的推力F正比于Sv2,其中v为风速、S为物块迎风面积.当风速变为2v0时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为( )
 如图,一质量为m的正方体物块置于风洞内的水平面上,其一面与风速垂直,当风速为v0时刚好能推动该物块.已知风对物块的推力F正比于Sv2,其中v为风速、S为物块迎风面积.当风速变为2v0时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为( )
如图,一质量为m的正方体物块置于风洞内的水平面上,其一面与风速垂直,当风速为v0时刚好能推动该物块.已知风对物块的推力F正比于Sv2,其中v为风速、S为物块迎风面积.当风速变为2v0时,刚好能推动用同一材料做成的另一正方体物块,则该物块的质量为( )| A. | 64m | B. | 32m | C. | 8m | D. | 4m |
2.一列简谐横波沿x轴正方向传播,t时刻的波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,T>0.6s,a、b、c、P、Q是介质中的质点,以下说法正确的是( )


| A. | 这列波的波速为50m/s | |
| B. | 质点a在这段时间内通过的路程为30cm | |
| C. | 质点c在这段时间内通过的路程为20cm | |
| D. | t+0.5s时刻,质点b、P的位移相同 | |
| E. | t+0.5s时刻,质点b的速度大于质点P的速度 |
19.关于曲线运动,下列叙述正确的是( )
| A. | 做曲线运动的物体速度方向在时刻改变,所以曲线运动不可能是匀变速运动 | |
| B. | 物体受到一个方向不断改变的力,才可能做曲线运动 | |
| C. | 物体不受外力,由于惯性而持续的运动不可能是曲线运动 | |
| D. | 做曲线运动的物体所受到的力的方向一定是变化的 |
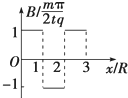
 如图所示,重力不计,质量为m,带正电且电荷量为q的粒子,在a点以某一初速度v0水平射入一个磁场区域沿曲线abcd运动,ab、bc、cd都是半径为R的圆弧,粒子在每段圆弧上的运动时间都是t,如果把由纸面穿出的磁场方向定为正值,则磁场区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随x变化关系图象应为下图所示的哪一个( )
如图所示,重力不计,质量为m,带正电且电荷量为q的粒子,在a点以某一初速度v0水平射入一个磁场区域沿曲线abcd运动,ab、bc、cd都是半径为R的圆弧,粒子在每段圆弧上的运动时间都是t,如果把由纸面穿出的磁场方向定为正值,则磁场区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随x变化关系图象应为下图所示的哪一个( )