题目内容
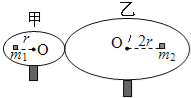
【题目】如图所示,甲、乙圆盘的半径之比为1:2,两水平圆盘紧靠在一起,乙靠摩擦随甲不打滑转动.两圆盘上分别放置质量为m1和m2的小物体,m1=2m2,两小物体与圆盘间的动摩擦因数相同.m1距甲盘圆心r,m2距乙盘圆心2r,此时它们正随盘做匀速圆周运动.下列判断正确的是( )
A. m1和m2的线速度之比为1:4
B. m1和m2的向心加速度之比为2:1
C. 随转速慢慢增加,m1先开始滑动
D. 随转速慢慢增加,m2先开始滑动
【答案】BC
【解析】试题分析:抓住两圆盘边缘的线速度大小相等,结合圆盘的半径关系得出两圆盘的角速度之比,从而根据向心加速度公式求出向心加速度之比.抓住最大静摩擦提供向心力求出发生滑动时的临界角速度,结合甲乙的角速度进行分析判断.
解:A、甲、乙两轮子边缘上的各点线速度大小相等,有:ω1R=ω22R,则得ω1:ω2=2:1,所以物块相对盘开始滑动前,m1与m2的角速度之比为2:1.
根据公式:v=ωr,所以:![]() .故A错误.
.故A错误.
B、根据a=ω2r得:m1与m2的向心加速度之比为 a1:a2=(ω12r):(ω222r)=2:1,故B正确.
C、D、根据μmg=mrω2=ma知,m1先达到临界角速度,可知当转速增加时,m1先开始滑动.故C正确,D错误.
故选:BC.

练习册系列答案
相关题目