题目内容
9. 如图所示,直角坐标系xOy的第二象限内有沿y轴负方向的匀强电场,x轴下方一半径为R、与x轴相切于O点的圆形区域内,有方向垂直纸面向外,磁感应强度大小为B=$\frac{2m{v}_{0}}{qR}$的匀强磁场,一质量为m、带电量为+q的带电粒子,从P(-2$\sqrt{3}$L,L)点以速度v0平行于x轴正方向向右射入,恰好经过O点进入圆形磁场区域,不计粒子重力,求:
如图所示,直角坐标系xOy的第二象限内有沿y轴负方向的匀强电场,x轴下方一半径为R、与x轴相切于O点的圆形区域内,有方向垂直纸面向外,磁感应强度大小为B=$\frac{2m{v}_{0}}{qR}$的匀强磁场,一质量为m、带电量为+q的带电粒子,从P(-2$\sqrt{3}$L,L)点以速度v0平行于x轴正方向向右射入,恰好经过O点进入圆形磁场区域,不计粒子重力,求:(1)匀强电场的电场强度;
(2)粒子第一次射出圆形磁场时的坐标;
(3)粒子从O点射入圆形磁场到第一次离开圆形磁场经历的时间.
分析 (1)粒子从P到O是类似平抛运动,根据类平抛运动的分运动公式列式分析即可;
(2)粒子在磁场中做匀速圆周运动,先根据牛顿第二定律列式求解轨道半径,画出运动轨迹,结合几何关系求解第一次射出磁场时的坐标;
(3)粒子在磁场中做匀速圆周运动,先结合几何关系确定圆心角,根据t=$\frac{θ}{2π}T$求解时间.
解答 解:(1)粒子从P到O是类似平抛运动,根据分位移公式,有:
x=2$\sqrt{3}$L=v0t ①
y=L=$\frac{1}{2}\frac{qE}{m}{t}^{2}$ ②
解得:
E=$\frac{m{v}_{0}^{2}}{6qL}$
(2)粒子从P到O是类似平抛运动,根据分速度公式,有:
vx=v0 ③
${v}_{y}=\frac{qE}{m}t$ ④
合速度:
v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$ ⑤
速度偏转角的正切值:
tanα=$\frac{{v}_{y}}{{v}_{0}}$ ⑥
联立①③④⑤⑥解得:
v=$\frac{2\sqrt{3}}{3}{v}_{0}$
α=30°
粒子在磁场中做匀速圆周运动,轨道半径为:
r=$\frac{mv}{qB}$=$\frac{m(\frac{2\sqrt{3}}{3}{v}_{0})}{q(\frac{2m{v}_{0}}{qR})}$=$\frac{\sqrt{3}}{3}R$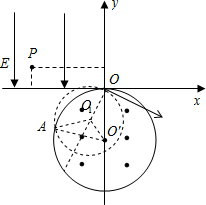 画出在磁场中的运动轨迹,如图所示:
画出在磁场中的运动轨迹,如图所示:
设第一次射出磁场时的坐标为(-x,-y);
图中三角形OO′O1中,∠OO1O′=∠OO′O1=30°
三角形OO′O1与三角形AO′O1是全等的,故:
A点坐标为:(-Rcos30°,-R+Rsin30°),即(-$\frac{\sqrt{3}}{2}R$,-$\frac{R}{2}$);
(3)粒子在磁场中做匀速圆周运动,圆心角为240°,故时间:
t=$\frac{2}{3}T=\frac{2}{3}×\frac{2πm}{qB}$=$\frac{4πm}{3q×\frac{2m{v}_{0}}{qR}}$=$\frac{2πR}{3{v}_{0}}$;
答:(1)匀强电场的电场强度为$\frac{m{v}_{0}^{2}}{6qL}$;
(2)粒子第一次射出磁场时的坐标为(-$\frac{\sqrt{3}}{2}R$,-$\frac{R}{2}$);
(3)粒子从O点射入磁场到第一次离开磁场经历的时间为$\frac{2πR}{3{v}_{0}}$.
点评 本题关键是明确粒子先做类似平抛运动,后做匀速圆周运动,根据类似平抛运动的分运动公式列式求解末速度大小和方向;在磁场中关键是画出轨迹,结合几何关系分,不难.

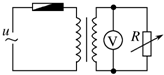 如图所示,一理想变压器原、副线圈的匝数比n1:n2=4:1,电源电压u=220$\sqrt{2}$sin314t(V),原线圈电路中接入熔断电流I0=1A的保险丝,副线圈电路中接入一可变电阻R,则( )
如图所示,一理想变压器原、副线圈的匝数比n1:n2=4:1,电源电压u=220$\sqrt{2}$sin314t(V),原线圈电路中接入熔断电流I0=1A的保险丝,副线圈电路中接入一可变电阻R,则( )| A. | 电压表的读数为77V | |
| B. | 当可变电阻R的阻值变大时,电源的输入功率变大 | |
| C. | 可变电阻R的阻值低于13.75Ω时保险丝将熔断 | |
| D. | 副线圈的输出功率一定是200W |
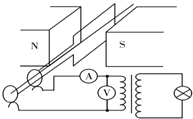 某兴趣小组用实验室的手摇发电机和理想变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,电压表示数是U1,额定电压为U2的灯泡正常发光,灯泡正常发光时电功率为 P,手摇发电机的线圈电阻是r,则有( )
某兴趣小组用实验室的手摇发电机和理想变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,电压表示数是U1,额定电压为U2的灯泡正常发光,灯泡正常发光时电功率为 P,手摇发电机的线圈电阻是r,则有( )| A. | 电流表的示数是$\frac{P}{{U}_{2}}$ | |
| B. | 变压器原副线圈的匝数比是U2:U1 | |
| C. | 变压器输入电压的瞬时值u=U2sin2πnt | |
| D. | 手摇发电机线圈中产生的电动势最大值是Em=$\sqrt{2}$(U1+$\frac{Pr}{{U}_{1}}$) |
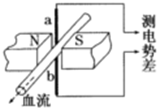 医生做某些特殊手术时,利用电磁血流计来监测通过动脉的血流速度,电磁血流计由一对电极a和b以及磁极N和S构成,磁极间的磁场是均匀的.使用时,两电极a、b与血管壁接触,两触点的连线、磁场方向和血流速度方向两两垂直,如图所示.由于血液中的正、负离子随血流一起在磁场中运动,电极a、b之间会有微小电势差.在达到平衡时,血管内部的电场可看做是匀强电场,血液中的离子所受的电场力和磁场力的合力为零,在某次监测中,两触点的距离为3.0mm,血管壁的厚度可忽略,两触电间的电势差为160μV,磁感应强度的大小为0.040T,则关于血流速度的近似值和电极a、b的正负以下说法正确的是( )
医生做某些特殊手术时,利用电磁血流计来监测通过动脉的血流速度,电磁血流计由一对电极a和b以及磁极N和S构成,磁极间的磁场是均匀的.使用时,两电极a、b与血管壁接触,两触点的连线、磁场方向和血流速度方向两两垂直,如图所示.由于血液中的正、负离子随血流一起在磁场中运动,电极a、b之间会有微小电势差.在达到平衡时,血管内部的电场可看做是匀强电场,血液中的离子所受的电场力和磁场力的合力为零,在某次监测中,两触点的距离为3.0mm,血管壁的厚度可忽略,两触电间的电势差为160μV,磁感应强度的大小为0.040T,则关于血流速度的近似值和电极a、b的正负以下说法正确的是( )| A. | a负,b正 | B. | 流速约为1.3m/s | C. | 流速约为2.7m/s | D. | a正,b负 |
 如图所示,A、B、C、D位于同一半径为r的竖直圆上,且AB⊥CD,在C点有一固定点电荷,电荷量为-Q,现从A点将一质量为m,电荷量为-q的带电小球由静止释放,该小球沿光滑绝缘轨道ADB运动到D点时速度为4$\sqrt{gr}$,规定电场中B点的电势为零,则在点电荷-Q形成的电场中下列说法正确的是(不计带电小球对电场的影响)( )
如图所示,A、B、C、D位于同一半径为r的竖直圆上,且AB⊥CD,在C点有一固定点电荷,电荷量为-Q,现从A点将一质量为m,电荷量为-q的带电小球由静止释放,该小球沿光滑绝缘轨道ADB运动到D点时速度为4$\sqrt{gr}$,规定电场中B点的电势为零,则在点电荷-Q形成的电场中下列说法正确的是(不计带电小球对电场的影响)( )| A. | D点电势为$\frac{7mgr}{q}$ | |
| B. | 小球在D点具有的电势能为正值 | |
| C. | O点电场强度大小是A点的2倍 | |
| D. | 小球通过D点时轨道对小球作用力大小为mg |
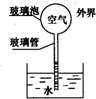 如图为物理兴趣小组设计的一种测温装置示意图,玻璃管的上端与导热良好的玻璃泡连通,下端插入水中,玻璃泡中封闭有一定量的空气,若玻璃管内水柱上升,则外界大气的变化可能是( )
如图为物理兴趣小组设计的一种测温装置示意图,玻璃管的上端与导热良好的玻璃泡连通,下端插入水中,玻璃泡中封闭有一定量的空气,若玻璃管内水柱上升,则外界大气的变化可能是( )| A. | 温度降低,压强增大 | B. | 温度升高,压强不变 | ||
| C. | 温度升高,压强减小 | D. | 温度不变,压强减小 |
 在测量金属丝电阻率的实验中,可供选用的器材如下:
在测量金属丝电阻率的实验中,可供选用的器材如下: 如图所示,玻璃三棱镜的横截面是边长为a的等边三角形,BC面沿竖直方向,O点为BC的中点,现用一束宽为a的单色平行光束水平射向AB及AC面,若玻璃三棱镜对此平行光束的折射率为$\sqrt{3}$,求:
如图所示,玻璃三棱镜的横截面是边长为a的等边三角形,BC面沿竖直方向,O点为BC的中点,现用一束宽为a的单色平行光束水平射向AB及AC面,若玻璃三棱镜对此平行光束的折射率为$\sqrt{3}$,求: 某同学用如图所示的装置通过半径相同的a、b两球的碰撞来验证碰撞中的动量守恒:
某同学用如图所示的装置通过半径相同的a、b两球的碰撞来验证碰撞中的动量守恒: