Question

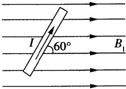如图所示，平行于纸面水平向右的匀强磁场，磁感应强度B=1T．位于纸面内的细直导线，长L=5m，通有I=3A的恒定电流．当导线与B成60°夹角时，发现其受到的安培力为零，则该区域同时存在的另一匀强磁场的磁感应强度B₁的可能值为（　　）

• A．

  3

  2

  T
• B．

  1

  2

  T
• C．2

  3

  T
• D．

  3

  3

  T

Answer 1

分析：当磁场方向与电流方向在同一直线上时，电流不受磁场力作用；
根据磁场的叠加原理，由平行四边形定则分析答题．

解答：解：通电导线所受磁场力为零，则电流方向与磁场方向平行，
说明该区域同时存在的另一匀强磁场B₂，并且B₂与B₁的合磁场的磁感应强度方向沿导线方向，
由三角形定则可知，当B₂与合磁场（通电导线）垂直时，磁场最小B_2最小=B₁sin60°，
则B₂≥B₁sin60°=

3

2

T，所以B₂的不可能值为

1

2

T与

3

3

T，故AC正确，BD错误；
故选AC．

点评：知道通电导线与磁场平行时导线所受磁场力为零是正确解题的关键；由矢量三角形法则求出磁感应强度的最小值即可正确解题．