题目内容
15.美国在2016年2月11日宣布“探测到引力波的存在”.天文学家通过观测双星轨道参数的变化来间接验证引力波的存在,证实了GW150914是两个黑洞并合的事件.GW150914是一个36倍太阳质量的黑洞和一个29倍太阳质量的黑洞并合事件.假设这两个黑洞绕它们连线上的某点做圆周运动,且这两个黑洞的间距缓慢减小.若该黑洞系统在运动过程中各自质量不变且不受其它星系的影响,则关于这两个黑洞的运动,下列说法正确的是( )| A. | 这两个黑洞做圆周运动的向心加速度大小始终相等 | |
| B. | 36倍太阳质量的黑洞比29倍太阳质量的黑洞运行的轨道半径小 | |
| C. | 这两个黑洞运行的线速度大小始终相等 | |
| D. | 随两个黑洞的间距缓慢减小,这两个黑洞运行的周期也在增大 |
分析 双星做匀速圆周运动具有相同的角速度,靠相互间的万有引力提供向心力,根据万有引力提供向心力公式以及线速度、向心加速度、角速度直接的关系判断即可.
解答 解:B、根据$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{1}^{\;}$可得${m}_{2}^{\;}=\frac{4{π}_{\;}^{2}{L}_{\;}^{2}}{G{T}_{\;}^{2}}{r}_{1}^{\;}$①
根据$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{2}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{2}^{\;}$可得${m}_{1}^{\;}=\frac{4{π}_{\;}^{2}{L}_{\;}^{2}}{G{T}_{\;}^{2}}{r}_{2}^{\;}$②
由①②知$\frac{{m}_{1}^{\;}}{{m}_{2}^{\;}}=\frac{{r}_{2}^{\;}}{{r}_{1}^{\;}}$,质量与轨道半径成反比,所以36倍太阳质量的黑洞轨道半径比29倍太阳质量的黑洞轨道半径小.故B正确;
A、根据$a={ω}_{\;}^{2}r$可知,角速度相等,质量大的半径小,所以质量大的向心加速度小,故A错误;
C、这两个黑洞共轴转动,角速度相等,根据v=ωr可以,质量大的半径小,所以质量大的线速度小.故C错误;
D、又:${m}_{1}^{\;}+{m}_{2}^{\;}=\frac{4{π}_{\;}^{2}{L}_{\;}^{2}}{{T}_{\;}^{2}}({r}_{1}^{\;}+{r}_{2}^{\;})$=$\frac{4{π}_{\;}^{2}{L}_{\;}^{3}}{G{T}_{\;}^{2}}$
当${m}_{1}^{\;}+{m}_{2}^{\;}$不变时,L减小,则T减小,即双星系统运行周期会随间距减小而减小,故D错误;
故选:B
点评 解决本题的关键知道双星靠相互间的万有引力提供向心力,应用万有引力定律与牛顿第二定律即可正确解题,难度不大,属于基础题.

 精英口算卡系列答案
精英口算卡系列答案| A. | 通常用光栅或棱镜来观察物体发光产生的光谱 | |
| B. | 可以利用光谱分析来鉴定物质的成分,但其灵敏度相对较低 | |
| C. | 所有元素产生的线状谱都是相同的 | |
| D. | 线状谱中的亮线反映了原子的特征 |
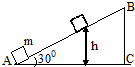 如图所示,一个质量为m的物体以某一速度从A点冲上倾角为300的斜面,其运动的加速度为$\frac{3}{4}$g,物体在斜面上上升的最大高度为h,则这过程中( )
如图所示,一个质量为m的物体以某一速度从A点冲上倾角为300的斜面,其运动的加速度为$\frac{3}{4}$g,物体在斜面上上升的最大高度为h,则这过程中( )| A. | 重力势能增加了$\frac{3}{4}$mgh | |
| B. | 机械能损失了$\frac{3}{2}$mgh | |
| C. | 动能减少了mgh | |
| D. | 若物体再次回到斜面底端,物体到斜面底端时的动能为$\frac{1}{2}$mgh |
| A. | 位移、速率和加速度都是标量 | |
| B. | 只有静止的物体才可以当作参考系 | |
| C. | 只有质量和体积都很小的物体才能看成质点 | |
| D. | 如果物体的形状和大小对所研究的问题属于无关或次要因素时,即可把物体看作质点 |
| A. | 在完全失重的情况下,密闭容器内的气体对器壁的顶部没有作用力 | |
| B. | 在绝热密闭的条件下压缩气体,气体的内能增加 | |
| C. | 由于液体表面分子间距离大于液体内部分子间的距离,液面分子间只有引力,没有斥力,所以液体表面具有收缩的趋势 | |
| D. | 一定温度下,饱和汽压是一定的,与体积无关 |
 中国北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)是中国自行研制的全球卫星导航系统,是继美国全球定位系统 (GPS)、俄罗斯格洛纳斯卫星导航系统(GLONASS)之后第三个成熟的卫星导航系统.预计2020年左右,北斗卫星导航系统将形成全球覆盖能力.如图所示是北斗导航系统中部分卫星的轨道示意图,己知a、b、c三颗卫星均做圆周运动,a是地球同步卫星,则( )
中国北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)是中国自行研制的全球卫星导航系统,是继美国全球定位系统 (GPS)、俄罗斯格洛纳斯卫星导航系统(GLONASS)之后第三个成熟的卫星导航系统.预计2020年左右,北斗卫星导航系统将形成全球覆盖能力.如图所示是北斗导航系统中部分卫星的轨道示意图,己知a、b、c三颗卫星均做圆周运动,a是地球同步卫星,则( )| A. | 卫星a的角速度小于c的角速度 | |
| B. | 卫星a的加速度小于b的加速度 | |
| C. | 卫星a的运行速度大于第一宇宙速度 | |
| D. | 卫星b的周期大于24 h |
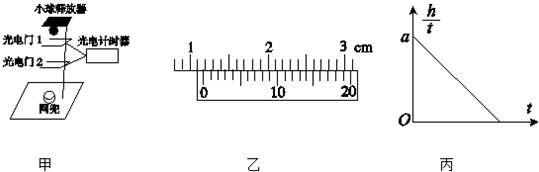
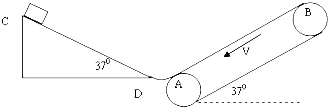 如图所示,物体从长为16m,倾角为37°的斜面顶端C由静止开始滑下,在斜面底端D用一段光滑的小圆弧滑上输送带AB上的A时速度的大小不变,物体与斜面、物体与输送带间的动摩擦因数均为0.5,输送带以2m/s的速度沿逆时针方向做匀速运动,输送带与水平方向的夹角也为37°,输送带足够长,( sin37°=0.6,cos37°=0.8)g取10m/s2.求
如图所示,物体从长为16m,倾角为37°的斜面顶端C由静止开始滑下,在斜面底端D用一段光滑的小圆弧滑上输送带AB上的A时速度的大小不变,物体与斜面、物体与输送带间的动摩擦因数均为0.5,输送带以2m/s的速度沿逆时针方向做匀速运动,输送带与水平方向的夹角也为37°,输送带足够长,( sin37°=0.6,cos37°=0.8)g取10m/s2.求 一个滑雪爱好者,质量m=60kg,v0=3m/s的初速度沿山坡匀加速滑下,山坡的倾角θ=37°,在t=4s的时间内滑下的路程x=52m,求
一个滑雪爱好者,质量m=60kg,v0=3m/s的初速度沿山坡匀加速滑下,山坡的倾角θ=37°,在t=4s的时间内滑下的路程x=52m,求