题目内容
长为L的细绳固定在O点，另一端系一质量为m的小球，开始时绳与水平方向成30°角，如图7-7-15所示.求小球由静止释放后运动到最低点C时的速度.
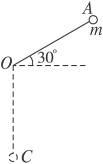
图7-7-15
解析:
如图所示，球到B点时细绳拉直，物体从A到B做自由落体运动，下落高度等于L，由机械能守恒定律得：
mgL=
mvB2 ①
物体到达B点时的速度为vB=
②
物体到达B点绷紧绳的瞬间，绳的拉力的作用使分速度v2损失掉，物体以分速度v1为初速度开始沿圆弧运动，从B到C机械能守恒，则有
mgL(1-cos60°)+mv12=mvc2 ③
v1=vBcos30° ④
所以，物体到达最低点C时的速度为
VC=
.
练习册系列答案
相关题目
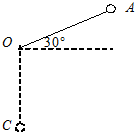一长L的细绳固定在O点，O点离地的高度大于L，另一端系质量为m的小球．开始时，线与水平方向夹角为30°，如图所示．求小球由静止释放后运动到最低点时的速度．
如图所示，两个质量均为m，带电量均为+q的小球A、B，一个固定在O点的正下方L处，另一个用长为L的细线悬挂在O点，静止时，细线与竖直方向的夹角为600，以下说法不正确的是（ ）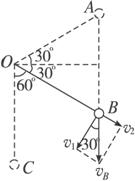
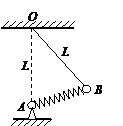A．F1 > F2