题目内容
(20分)一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状。此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面。如图所示,以沟底的O点为原点建立坐标系Oxy。已知,山沟竖直一侧的高度为2h,坡面的抛物线方程为y=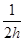 x2,探险队员的质量为m。人视为质点,忽略空气阻力,重力加速度为g。
x2,探险队员的质量为m。人视为质点,忽略空气阻力,重力加速度为g。
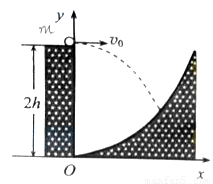
(1)求此人落到坡面时的动能;
(2)此人水平跳出的速度为多大时,他落在坡面时的动能最小?动能的最小值为多少?
【答案】
(1)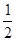 m (
m (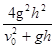 +v02)(2)
+v02)(2)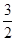 mgh
mgh
【解析】(1)由平抛运动规律,x=v0t,2h-y=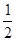 gt2,
gt2,
又y=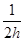 x2,
x2,
联立解得y=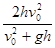 。
。
由动能定理,mg(2h-y)=Ek-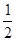 mv02,
mv02,
解得Ek = mg(2h-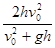 )+
)+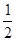 mv02=
mv02=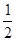 m
(
m
(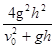 +v02)。
+v02)。
(2)Ek =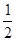 m
(
m
(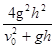 +v02)
=
+v02)
=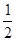 m
(
m
(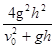 +v02+gh-gh)。
+v02+gh-gh)。
当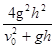 = v02+gh,即v0=
= v02+gh,即v0= 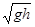 时,他落在坡面时的动能最小。
时,他落在坡面时的动能最小。
动能的最小值为Ek min=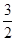 mgh。
mgh。

练习册系列答案
相关题目
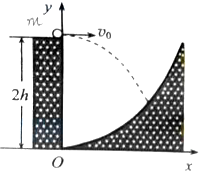 V一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状.此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面.如图所示,以沟底的O点为原点建立坐标系Oxy.已知,山沟竖直一侧的高度为2h,坡面的抛物线方程为y=
V一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状.此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面.如图所示,以沟底的O点为原点建立坐标系Oxy.已知,山沟竖直一侧的高度为2h,坡面的抛物线方程为y=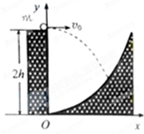 探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状.此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面.如图所示以沟底的O点为原点建立坐标系Oxy.已知,山沟竖直一侧的高度为2h,坡面的抛物线方程为y=
探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状.此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面.如图所示以沟底的O点为原点建立坐标系Oxy.已知,山沟竖直一侧的高度为2h,坡面的抛物线方程为y=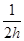 x2,探险队员的质量为m。人视为质点,忽略空气阻力,重力加速度为g。
x2,探险队员的质量为m。人视为质点,忽略空气阻力,重力加速度为g。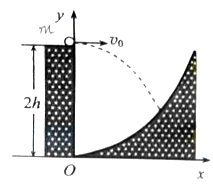
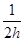 x2,探险队员的质量为m.人视为质点,忽略空气阻力,重力加速度为g.求此人落到坡面时的动能。
x2,探险队员的质量为m.人视为质点,忽略空气阻力,重力加速度为g.求此人落到坡面时的动能。