题目内容
如图所示,一边长为L的有界匀强磁场,其方向垂直纸面向里.有一质量为m带电量为q的正电荷从a点沿对角线ac以v0垂直射入磁场并垂直cd边射出磁场,求:
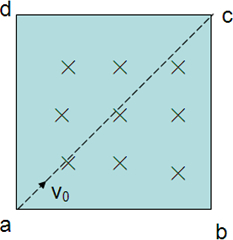
(1)该匀强磁场的磁感强度B的大小?
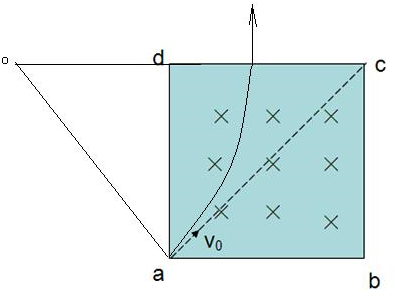
(2)若只改变初速度的大小,使得该带电粒子从d点射出磁场,则初速度的大小应为多少?

(1)该匀强磁场的磁感强度B的大小?
(2)若只改变初速度的大小,使得该带电粒子从d点射出磁场,则初速度的大小应为多少?
分析:(1)根据几何关系,确定已知长度与轨道半径的关系,再由洛伦兹力提供向心力,结合牛顿第二定律,即可求解;
(2)同理,由几何关系,结合牛顿第二定律,即可求解.
(2)同理,由几何关系,结合牛顿第二定律,即可求解.
解答:解:(1)带电粒子在磁场中做匀速圆周运动垂直dc射出磁场,表明圆心一定在cd的延长线和过a点且垂直ac的直线的交点.
由几何关系:
r=
=
L①
洛仑兹力提供向心力,则:
qv0B=m
②
由①②得:B=
;
(2)若改变初速度的大小,使粒子从d点射出,半径r1为:
r1=L sin45°=
L
由qvB=
得:v=
;
答:(1)该匀强磁场的磁感强度B的大小
;
(2)若只改变初速度的大小,使得该带电粒子从d点射出磁场,则初速度的大小应为
.
由几何关系:

r=
| L |
| sin45° |
| 2 |
洛仑兹力提供向心力,则:
qv0B=m
| v0 |
| r |
由①②得:B=
| ||
| 2qL |
(2)若改变初速度的大小,使粒子从d点射出,半径r1为:
r1=L sin45°=
| ||
| 2 |
由qvB=
| mv2 |
| r1 |
得:v=
| ||
| 2 |
| qBL |
| m |
答:(1)该匀强磁场的磁感强度B的大小
| ||
| 2qL |
(2)若只改变初速度的大小,使得该带电粒子从d点射出磁场,则初速度的大小应为
| ||
| 2 |
| qBL |
| m |
点评:考查牛顿第二定律的应用,掌握洛伦兹力与向心力的表达式,注意几何关系的正确建立.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
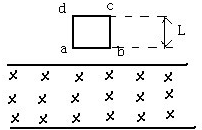 如图所示有一边长为L的正方形线框abcd,从某高度处自由下落,在其下方有一个宽度大于L的匀强磁场,下列过程中产生电流的是( )
如图所示有一边长为L的正方形线框abcd,从某高度处自由下落,在其下方有一个宽度大于L的匀强磁场,下列过程中产生电流的是( )| A、线框进入磁场的过程 | B、线框全部进入磁场到开始出磁场的过程 | C、线框出磁场的过程 | D、运动的整个过程. |
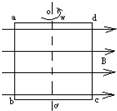 如图所示,一边长为L的正方形线圈abcd绕对称轴在匀强磁场中转动,转速为n,匝数为N,磁感应强度为B,则从图示位置开始计时,下列说法正确的是( )
如图所示,一边长为L的正方形线圈abcd绕对称轴在匀强磁场中转动,转速为n,匝数为N,磁感应强度为B,则从图示位置开始计时,下列说法正确的是( )| A、开始时通过线圈的磁通量最大 | B、开始时通过线圈的磁通量变化率最大 | C、转过900时感应电动势最大 | D、转过900时感应电动势方向发生变化 |
 (2011?佛山二模)如图所示,一边长为L的正方形导线框,匀速穿过宽2L的匀强磁场区域.取它刚进入磁场的时刻为t=0,则在下图中,能正确反映线框感应电流i随时间t变化规律的是(规定线框中电流沿逆时针方向为正)( )
(2011?佛山二模)如图所示,一边长为L的正方形导线框,匀速穿过宽2L的匀强磁场区域.取它刚进入磁场的时刻为t=0,则在下图中,能正确反映线框感应电流i随时间t变化规律的是(规定线框中电流沿逆时针方向为正)( )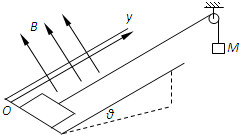 如图所示,一边长为L,质量为m,电阻为R的正方形金属框放置在倾角为θ的光滑绝缘斜面的底端,并用细线通过轻质定滑轮与质量为M的重物相连.磁场的方向垂直金属框平面,磁感应强度的大小只随y方向变化,规律为B=B0+ky,k为大于零的常数.假设运动过程中金属框总有两条边与y轴平行,且金属框不转动,当金属框沿y轴方向运动距离为h时速度达到最大.不计空气阻力,斜面和磁场区域足够大,重力加速度为g.求:
如图所示,一边长为L,质量为m,电阻为R的正方形金属框放置在倾角为θ的光滑绝缘斜面的底端,并用细线通过轻质定滑轮与质量为M的重物相连.磁场的方向垂直金属框平面,磁感应强度的大小只随y方向变化,规律为B=B0+ky,k为大于零的常数.假设运动过程中金属框总有两条边与y轴平行,且金属框不转动,当金属框沿y轴方向运动距离为h时速度达到最大.不计空气阻力,斜面和磁场区域足够大,重力加速度为g.求: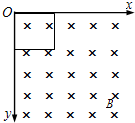 如图所示,一边长为L、质量为m、电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面,磁感应强度的大小随y的变化规律为B=B0+ky(k为恒定常数且大于零),同一水平面上磁感应强度相同.现将方框从y=0处自由下落,重力加速度为g,设磁场区域足够大,不计空气阻力,则方框中感应电流的方向为
如图所示,一边长为L、质量为m、电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面,磁感应强度的大小随y的变化规律为B=B0+ky(k为恒定常数且大于零),同一水平面上磁感应强度相同.现将方框从y=0处自由下落,重力加速度为g,设磁场区域足够大,不计空气阻力,则方框中感应电流的方向为