题目内容
 (2010?普陀区一模)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求:
(2010?普陀区一模)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布.),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求:(1)C、O间的电势差UCO;
(2)O点处的电场强度E的大小;
(3)小球p经过O点时的加速度;
(4)小球p经过与点电荷B等高的D点时的速度.
分析:要求解电势差,我们应该去想电势差与电场力做功的关系,
要求解电场力做功我们想到运用动能定理.
一个物理量的求解我们应该去找出与这个物理量有关的已知物理量,可以根据所求的物理量反向思考.
小球p经过O点时受力分析,根据电场强度的定义式求解电场强度.
对于变加速直线运动求速度,我们应该首选动能定理求解.
要求解电场力做功我们想到运用动能定理.
一个物理量的求解我们应该去找出与这个物理量有关的已知物理量,可以根据所求的物理量反向思考.
小球p经过O点时受力分析,根据电场强度的定义式求解电场强度.
对于变加速直线运动求速度,我们应该首选动能定理求解.
解答: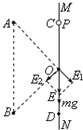 解:(1)小球p由C运动到O时,由动能定理,
解:(1)小球p由C运动到O时,由动能定理,
得:mgd+qUCO=
mv2-0①
∴UCO=
②
(2)小球p经过O点时受力如图:由库仑定律得:F1=F2=k
它们的合力为:F=F1cos45°+F2cos45°=
③
∴O点处的电场强度E=
=
,④
(3)由牛顿第二定律得:mg+qE=ma⑤
∴a=g+
⑥
(4)小球p由O运动到D的过程,由动能定理得:mgd+qUOD=
m
-
mv2⑦
由电场特点可知:UCO=UOD⑧
联立①⑦⑧解得:vD=
v⑨
答:(1)C、O间的电势差UCO是
(2)O点处的电场强度E的大小是
;
(3)小球p经过O点时的加速度是
;
(4)小球p经过与点电荷B等高的D点时的速度是
v.
 解:(1)小球p由C运动到O时,由动能定理,
解:(1)小球p由C运动到O时,由动能定理,得:mgd+qUCO=
| 1 |
| 2 |
∴UCO=
| mv2-2mgd |
| 2q |
(2)小球p经过O点时受力如图:由库仑定律得:F1=F2=k
(
|
它们的合力为:F=F1cos45°+F2cos45°=
| ||
| 2d2 |
∴O点处的电场强度E=
| F |
| q |
| ||
| 2d2 |
(3)由牛顿第二定律得:mg+qE=ma⑤
∴a=g+
| ||
| 2md2 |
(4)小球p由O运动到D的过程,由动能定理得:mgd+qUOD=
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
由电场特点可知:UCO=UOD⑧
联立①⑦⑧解得:vD=
| 2 |
答:(1)C、O间的电势差UCO是
| mv2-2mgd |
| 2q |
(2)O点处的电场强度E的大小是
| ||
| 2d2 |
(3)小球p经过O点时的加速度是
| ||
| 2md2 |
(4)小球p经过与点电荷B等高的D点时的速度是
| 2 |
点评:选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.
了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (2010?普陀区一模)如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面以速度v匀速运动时,以下说法中正确的是( )
(2010?普陀区一模)如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面以速度v匀速运动时,以下说法中正确的是( ) (2010?普陀区一模)如图所示,叠放在一起的A、B两绝缘小物块放在水平向右的匀强电场中,其中B带正电q而A不带电,它们一切沿绝缘水平面以某一速度匀速运动.现突然使B带电量消失,同时A带上正电q,则A、B的运动状态可能为( )
(2010?普陀区一模)如图所示,叠放在一起的A、B两绝缘小物块放在水平向右的匀强电场中,其中B带正电q而A不带电,它们一切沿绝缘水平面以某一速度匀速运动.现突然使B带电量消失,同时A带上正电q,则A、B的运动状态可能为( ) (2010?普陀区一模)如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为,导轨平面与水平面的夹角=30°,导轨电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面向上.长为 的金属棒 垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为、电阻为r=R.两金属导轨的上端连接一个灯泡,灯泡的电阻RL=R,重力加速度为g.现闭合开关S,给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F=mg的恒力,使金属棒由静止开始运动,当金属棒达到最大速度时,灯泡恰能达到它的额定功率.求:
(2010?普陀区一模)如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为,导轨平面与水平面的夹角=30°,导轨电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面向上.长为 的金属棒 垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为、电阻为r=R.两金属导轨的上端连接一个灯泡,灯泡的电阻RL=R,重力加速度为g.现闭合开关S,给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F=mg的恒力,使金属棒由静止开始运动,当金属棒达到最大速度时,灯泡恰能达到它的额定功率.求: