题目内容
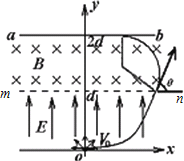
【题目】如图所示，在xoy坐标系坐标原点O处有一点状的放射源，它向xoy平面内的x轴上方各个方向发射α粒子，α粒子的速度大小均为v0，在0＜y＜d的区域内分布有指向y轴正方向的匀强电场，场强大小为
，其中q与m分别为α粒子的电量和质量；在d＜y＜2d的区域内分布有垂直于xoy平面向里的匀强磁场，mn为电场和磁场的边界．ab为一块很大的平面感光板垂直于xoy平面且平行于x轴，放置于y=2d处，如图所示．观察发现此时恰好无粒子打到ab板上．（不考虑α粒子的重力及粒子间的相互作用），求：
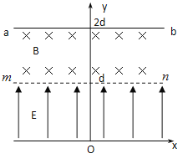
（1）α粒子通过电场和磁场边界mn时的速度大小及此时距y轴的最大距离；
（2）磁感应强度B的大小；
（3）将ab板至少向下平移多大距离才能使所有的粒子均能打到板上？此时ab板上被α粒子打中的区域的长度．
【答案】（1）
（2）
（3）
【解析】
试题分析：（1）α粒子在电场的作用下加速运动，根据动能定理： 
（2分）
代入数据可得： （1分）
由题意可知初速度方向与x轴平行的粒子通过边界mn时距y轴最远，由类平抛知识：
在竖直方向： 
其中
在水平方向：
联立以上解得： （3分）
（2）根据上题结果可知：对于沿x轴正方向射出的粒子进入磁场时与x轴正方向夹角：
可得
（1分）
若此粒子不能打到ab板上，则所有粒子均不能打到ab板，因此此粒子轨迹与ab板相切是临界条件，由几何关系可得：
解得： 
（2分）
由洛伦兹力提供向心力：
（1分）
可得： （1分）
（3）由分析可知沿x轴负方向射出的粒子若能打到ab板上，则所有粒子均能打到板上．其临界情况就是此粒子轨迹恰好与ab板相切． （2分）
由分析可知此时磁场宽度为原来的
， （2分）
则：ab板至少向下移动： （1分）
沿x轴正方向射出的粒子打在ab板的位置粒子打在ab板区域的右边界
由几何知识可知：ab板上被粒子打中区域的长度： 
（2分）
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
