题目内容
(08年黄桥中学三模)(16分)如图所示,光滑的平行金属导轨CD与EF间距为L=1m,与水平夹角为θ=300,导轨上端用导线CE连接(导轨和连接线电阻不计),导轨处在磁感应强度为B=0.1T、方向垂直于导轨平面向上的匀强磁场中.一根电阻为R=lΩ 的金属棒MN两端有导电小轮搁在两导轨上,棒上有吸水装置P.取沿导轨向下为x轴正方向,坐标原点在CE中点.开始时棒处在x=0位置(即与CE重合),棒的起始质量不计.当棒自静止起下滑时,便开始吸水,质量逐渐增大,设棒质量的增大与位移x的平方根成正比,即![]() ,k为一常数,
,k为一常数,![]() .求:
.求:
⑴猜测金属棒下滑过程中做的是什么性质的运动,并加以证明.
⑵金属棒下滑2 m位移时速度为多大?
 ⑶金属棒下滑2 m位移过程中,流过棒的电荷量是多少?
⑶金属棒下滑2 m位移过程中,流过棒的电荷量是多少?
解析:
⑴由于棒从静止开始运动,因此首先可以确定棒开始阶段做加速运动,然后通过受力分析,看看加速度可能如何变化?如图所示,棒在下滑过程中沿导轨方向有向下的重力分力mgsinθ和向上的安培力F.由于m随位移x增大而增大,所以,mgsinθ是一个变力;而安培力与速度有关,也随位移增大而增大.如果两个力的差值恒定,即合外力是恒力的话,棒有可能做匀加速运动.不妨假设棒做的是匀加速运动,且设下滑位移x时的加速度为ai,根据牛顿第二定律,有
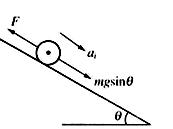
![]()
安培力F=ILB,![]() ,所以
,所以![]() ,
,
有 ![]() ①
①
假设棒做匀加速运动.则瞬时速度 ![]() ,
,
由于![]() ,代入后得到
,代入后得到
![]() ②
②
消去![]() 后得到
后得到
![]() ③
③
从上述方程可以看出ai的解是一个定值,与位移x无关,这表明前面的假设成立.棒的运动确实是匀加速运动.若本问题中m不与![]() 成正比,代人牛顿第二定律方程后,
成正比,代人牛顿第二定律方程后,![]() 不能消去,加速度ai就与x有关,从而说明ai是一个变量,得到是一个不能白洽的结果,则表明前面的假设不能成立.
不能消去,加速度ai就与x有关,从而说明ai是一个变量,得到是一个不能白洽的结果,则表明前面的假设不能成立.
⑵为了求棒下滑2 m时的速度,应先求出棒的加速度.将题目给出的数据代入③式得到
![]()
化简有 ![]() ④
④
令![]() ,则④式可写作
,则④式可写作
![]()
解得 a=4.69m/s2.
根据匀变速运动规律,
![]()
⑶金属棒下滑2m过程中,流过棒的电量可以用![]() 求解。
求解。
![]()
另一种解法是用![]() 求解。棒中瞬时电流
求解。棒中瞬时电流![]() 。由于v是随时间均匀增加的,所以电流也随时间均匀增加,棒下滑2m位移所需时间为
。由于v是随时间均匀增加的,所以电流也随时间均匀增加,棒下滑2m位移所需时间为![]() ,在这段时间内平均电流
,在这段时间内平均电流![]() ,所以
,所以![]() ,所得的结果与前面相同
,所得的结果与前面相同
。