题目内容
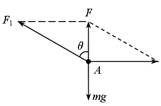
(14分)如图所示,用长为L的细线OA和水平细线将质量为m的小球系住,此时细线OA与竖直方向成θ= 60°角。小球视为质点,重力加速度大小为g,不计空气阻力。
(1)求细线OA对小球的拉力大小F1;
(2)烧掉水平细线后,小球下摆,求小球经过最低点B时细线OA对小球的拉力大小F2。
(1)求细线OA对小球的拉力大小F1;
(2)烧掉水平细线后,小球下摆,求小球经过最低点B时细线OA对小球的拉力大小F2。

(1)F1= 2mg
(2)F2= 2mg
(2)F2= 2mg
(1)小球处于平衡状态,受力如图所示,则有
F1=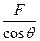 (2分)
(2分)
而 F=mg (2分)
得 F1= 2mg (2分)
(2)设到达最低点B时小球的速度大小为υ。则小球下摆过程,根据机械能守恒有
mgL(1 - cosθ) =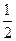 mυ2 (3分)
mυ2 (3分)
在最低点B时,有
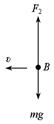
F2–mg=m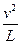 (3分)
(3分)
F2= 2mg (2分)

F1=
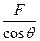 (2分)
(2分)而 F=mg (2分)
得 F1= 2mg (2分)
(2)设到达最低点B时小球的速度大小为υ。则小球下摆过程,根据机械能守恒有
mgL(1 - cosθ) =
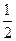 mυ2 (3分)
mυ2 (3分)在最低点B时,有

F2–mg=m
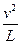 (3分)
(3分)F2= 2mg (2分)

练习册系列答案
相关题目

 糙的水平地面上,在斜劈上放一重为G的物块,物块静
糙的水平地面上,在斜劈上放一重为G的物块,物块静 止在斜劈上,今用一竖直向下的力F作用于物块上,下列说法正确的是 ( )
止在斜劈上,今用一竖直向下的力F作用于物块上,下列说法正确的是 ( )

 .则F的大小
.则F的大小
 mg
mg mg
mg mg
mg 两根竖直的轻弹簧各有一端固定,另一端共同静止地系住一重为10N的球。若撤去弹簧b,撤去瞬间球所受到的合力大小为2N;若撤去弹簧
两根竖直的轻弹簧各有一端固定,另一端共同静止地系住一重为10N的球。若撤去弹簧b,撤去瞬间球所受到的合力大小为2N;若撤去弹簧 ,则撤去瞬间球所受到的合力大小可能为 ( )
,则撤去瞬间球所受到的合力大小可能为 ( )

