题目内容
图6，金属棒P从高h处以速度v0沿光滑弧形平行导轨下滑，进入轨道的水平部分后，在自下而上垂直于导轨平面的匀强磁场中运动，磁感应强度为B.在轨道的水平部分原来静止放着另一根金属棒Q，已知mP∶mQ=3∶4，假设导轨足够长.试问:
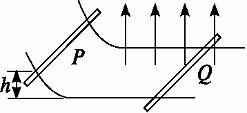
（1）当P棒进入磁场后，P、Q棒各做什么运动？?
（2）P棒刚进入磁场时，P、Q两棒加速度之比为多少？?
（3）若两棒始终没有碰撞，求P和Q的最大速度；?
（4）在整个过程中回路中消耗的电能是多少？（已知mP）
(1)减速运动 加速运动 (2)4∶3 
解析:
解本题关键应抓住:（1）当P、Q两棒速度相等时，回路电流为零，P、Q不受安培力做匀速直线运动；（2）P、Q两棒所受合外力为零，动量守恒；（3）全过程能量守恒.
P棒沿光滑弧面下滑，直到进入水平轨道之前，整个系统机械能守恒.对P棒
所以
P棒刚进入磁场时速度最大，其后由于P棒切割磁感线使整个回路产生感应电流，反过来，由于P、Q棒中有电流存在，两棒受安培力作用而分别做减速运动和加速运动，直到两棒速度相同为止，该速度即为Q棒最大速度.由于两棒所受的安培力F=BIl，尽管回路中感应电流不断变化，但两棒通过电流始终相等，所以两棒所受安培力大小始终相等，这样两棒运动的加速度之比始终为: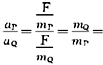 
在这一阶段中，两棒运动速度不断变化，回路中的感应电动势、感应电流、安培力、两棒的加速度都在不断变化.用牛顿运动定律求两棒速度是非常困难的，但若把两棒看成一个运动系统，这样根据动量守恒定律mPvP=(mP+mQ)v，所以
即Q的最大速度.
两棒速度相同后，穿过整个回路的磁通量不再变化，回路中无感应电流，两棒不再受安培力作用，在光滑水平轨道上各自做匀速运动，整个系统无能量消耗.要计算从P棒下滑到两棒均以v滑动的全过程中回路消耗的电能，因感应电流为变量，无法用Q=I2Rt计算，但根据能量守恒，回路消耗的电能即系统减少的机械能，所以Q=mPgh+
