题目内容
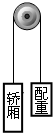如图所示，电梯由质量为1×103kg的轿厢、质量为8×102kg的配重、定滑轮和钢缆组成，轿厢和配重分别系在一根绕过定滑轮的钢缆两端，在与定滑轮同轴的电动机驱动下电梯正常工作，定滑轮与钢缆的质量可忽略不计，重力加速度g=10m/s2．在轿厢由静止开始以2m/s2的加速度向上运行1s的过程中，电动机对电梯共做功为（ ）分析：根据牛顿第二定律与运动学公式，求出各自牵引力的大小，根据做功的正负，从而求出牵引力做的总功．
解答：解：根据牛顿第二定律得，F-Mg=Ma，解得F=Mg+Ma=1000×12N=12000N，
静止开始以2m/s2的加速度向上运行1s的过程中，发生位移为h=
at2=
×2×12m=1m；
则起重机对轿厢做正功W=Fh=12000J．
对于质量为8×102kg的配重，牵引力做负功，其值为W′．
根据牛顿第二定律得，F′-mg=ma，解得F′=mg-ma=800×8N=6400N，
因此起重机对配重做负功W′=F′h=-6400J．
所以电动机对电梯共做功为12000J-6400J=5600J，故D正确，ABC错误；
故选D
静止开始以2m/s2的加速度向上运行1s的过程中，发生位移为h=
| 1 |
| 2 |
| 1 |
| 2 |
则起重机对轿厢做正功W=Fh=12000J．
对于质量为8×102kg的配重，牵引力做负功，其值为W′．
根据牛顿第二定律得，F′-mg=ma，解得F′=mg-ma=800×8N=6400N，
因此起重机对配重做负功W′=F′h=-6400J．
所以电动机对电梯共做功为12000J-6400J=5600J，故D正确，ABC错误；
故选D
点评：本题通过牛顿第二定律，结合功的公式进行求解，也可以通过动能定理求出起重机对物体做功的大小．
练习册系列答案
相关题目
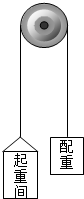（2007?武汉三模）如图所示，电梯由质量为1×103kg的起重间、质量为8×102kg的配重、定滑轮和钢缆组成，起重间和配重分别系在一根绕过定滑轮的钢缆两端，在与定滑轮同轴的电动机驱动下电梯正常工作，起重间由静止开始以2m/s2的加速度向上运行1s，在此时间内电动机对电梯做功（忽略定滑轮与钢缆的质量，g取10m/s2）（ ）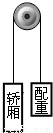
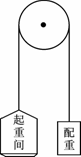
kg的起重间与一个质量为8
kg的配重、定滑轮和钢缆组成，起重间和配重分别系在一根绕过定滑轮的钢缆两端，在与定滑轮同轴的电动机驱动下电梯正常工作，起重间由静止开始以2m/s2的加速度向上运行1s，在此时间内电动机对电梯做功（忽略滑轮与钢缆的质量，g取10m/s2）（）
J D、2.16
如图所示，电梯由质量为1×103kg的轿厢、质量为8×102kg的配重、定滑轮和钢缆组成，轿厢和配重分别系在一根绕过定滑轮的钢缆两端，在与定滑轮同轴的电动机驱动下电梯正常工作，定滑轮与钢缆的质量可忽略不计，重力加速度g＝10 m/s2。在轿厢由静止开始以2m/s2的加速度向上运行1s的过程中，电动机对电梯共做功为 （ ）