题目内容
 如图所示,滑雪运动员质量m=75kg,沿倾角θ=30°的山坡匀加速滑下,经过1s的时间速度由3m/s增加到7m/s,忽略空气阻力,g=10m/s2,求:
如图所示,滑雪运动员质量m=75kg,沿倾角θ=30°的山坡匀加速滑下,经过1s的时间速度由3m/s增加到7m/s,忽略空气阻力,g=10m/s2,求:(1)运动员下滑过程中的加速度大小;
(2)运动员在这段时间内沿山坡下滑的距离;
(3)运动员受到的阻力.
分析:(1)根据速度时间公式求出运动员的加速度.
(2)根据位移时间公式求出运动员的位移.
(3)根据牛顿第二定律求出阻力的大小.
(2)根据位移时间公式求出运动员的位移.
(3)根据牛顿第二定律求出阻力的大小.
解答:解:(1)由运动学速度公式vt=v0+at,可得运动员的加速度:
a=
=
m/s2=4m/s2.
(2)运动员的位移:x=v0t+
at2=(3×1+
×4×12)m=5m.
(3)根据牛顿第二定律得,
mgsinθ-f=ma,可解出阻力
f=mgsinθ-ma=(75×10×0.5-75×4)N=75N.
答:(1)运动员下滑过程中的加速度大小为4m/s2.
(2)运动员在这段时间内沿山坡下滑的距离为5m.
(3)运动员受到的阻力为75N.
a=
| vt-v0 |
| t |
| 7-3 |
| 1 |
(2)运动员的位移:x=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据牛顿第二定律得,
mgsinθ-f=ma,可解出阻力
f=mgsinθ-ma=(75×10×0.5-75×4)N=75N.
答:(1)运动员下滑过程中的加速度大小为4m/s2.
(2)运动员在这段时间内沿山坡下滑的距离为5m.
(3)运动员受到的阻力为75N.
点评:本题考查了牛顿第二定律和运动学公式的运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
 如图所示,滑雪运动员由斜坡高速向下滑行时其速度-时间图象如图乙所示,则由图象中AB段曲线可知,运动员在此过程中( )
如图所示,滑雪运动员由斜坡高速向下滑行时其速度-时间图象如图乙所示,则由图象中AB段曲线可知,运动员在此过程中( ) 如图所示,滑雪运动员沿倾角为30°的滑雪道匀速下滑( )
如图所示,滑雪运动员沿倾角为30°的滑雪道匀速下滑( )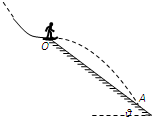 如图所示,滑雪运动员以一定的速度从一平台的O点水平飞出,落地点A到飞出点O的距离OA=27m,山坡与水平面的夹角θ=37°.不计空气阻力.(已知sin37°=0.6,cos37°=0.8)求:
如图所示,滑雪运动员以一定的速度从一平台的O点水平飞出,落地点A到飞出点O的距离OA=27m,山坡与水平面的夹角θ=37°.不计空气阻力.(已知sin37°=0.6,cos37°=0.8)求: 如图所示,滑雪运动员沿倾角为θ的山坡匀加速滑下,经过 1s 的时间,速度由3m/s 增加7m/s,求:
如图所示,滑雪运动员沿倾角为θ的山坡匀加速滑下,经过 1s 的时间,速度由3m/s 增加7m/s,求: