题目内容
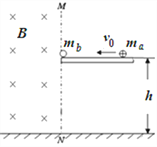
【题目】如图所示,水平地面上方MN边界左侧存在垂直纸面向里的匀强磁场和沿竖直方向的匀强电场(图中未画出),磁感应强度B=1.0T,边界右侧离地面高h=0.45m处由光滑绝缘平台,右边有一带正电的a球,质量![]() =0.1kg、电量q=0.1C,以初速度
=0.1kg、电量q=0.1C,以初速度![]() =0.9m/s水平向左运动,与大小相同但质量为
=0.9m/s水平向左运动,与大小相同但质量为![]() =0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后a球恰好做匀速圆周运动,两球均视为质点,
=0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后a球恰好做匀速圆周运动,两球均视为质点, ![]() ,求:
,求:
(1)电场强度的大小和方向;
(2)碰后两球分别在电磁场中运动的时间;
(3)碰后两球落地点相距多远;
【答案】(1)10N/C;方向向上;(2)a球离开电磁场用时2.1s;tb=0.30s;(3)0.10m
【解析】(1)a球碰后在叠加场中做匀速圆周运动,满足mg=qE
可得E=10N/C
a球带正电,电场力方向向上,则电场强度方向向上.
(2)a球与b球发生碰撞,由动量守恒定律得
mav0=mava+mbvb
由能量守恒定律得![]() mav02=
mav02=![]() mava2+
mava2+![]() mbvb2
mbvb2
解得:va=0.3m/s
vb=1.2m/s
对a球,洛仑兹力提供向心力![]()
可得![]()
设a球落地点与圆心的连线和地面夹角为θ,由几何关系有h=r+rsinθ
可得![]()
故a球离开电磁场用时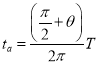 ,
, ![]() 代入得ta=
代入得ta=![]() πs≈2.1s
πs≈2.1s
b球不带电,碰撞后做平抛运动,竖直方向有 h=![]() gtb2 代入得tb=0.3s
gtb2 代入得tb=0.3s
(3)对a球,xa=rcosθ=0.15![]() m
m
对b球,xb=vbtb=0.36m
故两球相距:△x=xb-xa≈0.10m

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目