��Ŀ����
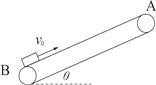
����Ŀ����ͼ��ʾ��һ������Ϊm=2kg��С������ɿ����ʵ�����ʼʱ��ֹ�ڸ߶�h=0��2m������L=4m������M=1kg��ľ��AB�������A����C��ΪAB���е㡣ľ���ϱ���AC���ֲִڣ�CB���ֹ⻬���±�����ˮƽ�����Ķ�Ħ������![]() =0��1���ֶ�С���ʩ��һ��ˮƽ���ҵĴ�СΪF=12N�ĺ�����ľ���С���ǡ���ܱ�����Ծ�ֹ����֪���Ħ�������ڻ���Ħ�������������ٶ�gȡ10m/s2
=0��1���ֶ�С���ʩ��һ��ˮƽ���ҵĴ�СΪF=12N�ĺ�����ľ���С���ǡ���ܱ�����Ծ�ֹ����֪���Ħ�������ڻ���Ħ�������������ٶ�gȡ10m/s2

��1����С�����ľ���ϱ���AC���ּ�Ķ�Ħ������![]()
��2�������С���ʩ��һ��ˮƽ���ҵĴ�СΪF=14N�ĺ�������С����˶�����C��ʱ��С����ľ����ٶȸ�Ϊ����?
��3���ڵ���2���ʵ�����£���С��鵽��C��ʱ��ȥF����С������ʱ��ľ��B�˵�ˮƽ���롣
���𰸡���1��![]() ����2��8m/s��6m/s��
����2��8m/s��6m/s��
��������
�����������1����Ϊľ���С���ǡ���ܱ�����Ծ�ֹ���������Ħ�������ڻ���Ħ����������ţ�ٵڶ�����
�����壺![]()
��С��飺![]()
��ã�![]()
��2����F=14N����ʱС�����ľ�巢����Ի�������ľ����������������ţ�ٵڶ�������
![]()
�ɵ�ľ����ٶ�a2=3m/s2
�������![]()
�ɵ�С�����ٶ� a3=4m/s2
����λ�ƹ�ϵ��![]() ,�ɵ�t1=2s
,�ɵ�t1=2s
��С��鵽C��ʱС����ľ����Ե��ٶȷֱ�Ϊv1��v2
![]() ��
��![]()
��3����С��鵽��C�㳷ȥF��С���ˮƽ����������������ֱ���˶���ľ���ܵ������Ħ�������䣬��ţ�ٵڶ����ɵã�![]() ���������ݵ���
���������ݵ���![]()
���پ���t2С����뿪ľ�壬�� ![]()
�������ݵ���![]()
�뿪ʱľ����ٶ���![]()
С����뿪ľ�����ƽ���˶���ƽ���˶�ʱ����![]()
�ù���С�����ˮƽ�����λ�ƣ�![]()
ľ����ˮƽ�������ȼ����˶�������ٶȣ�![]()
![]() ʱ����ľ���λ����
ʱ����ľ���λ����![]()
����С������ʱ��ľ��B�˵�ˮƽ���룺![]()

 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�